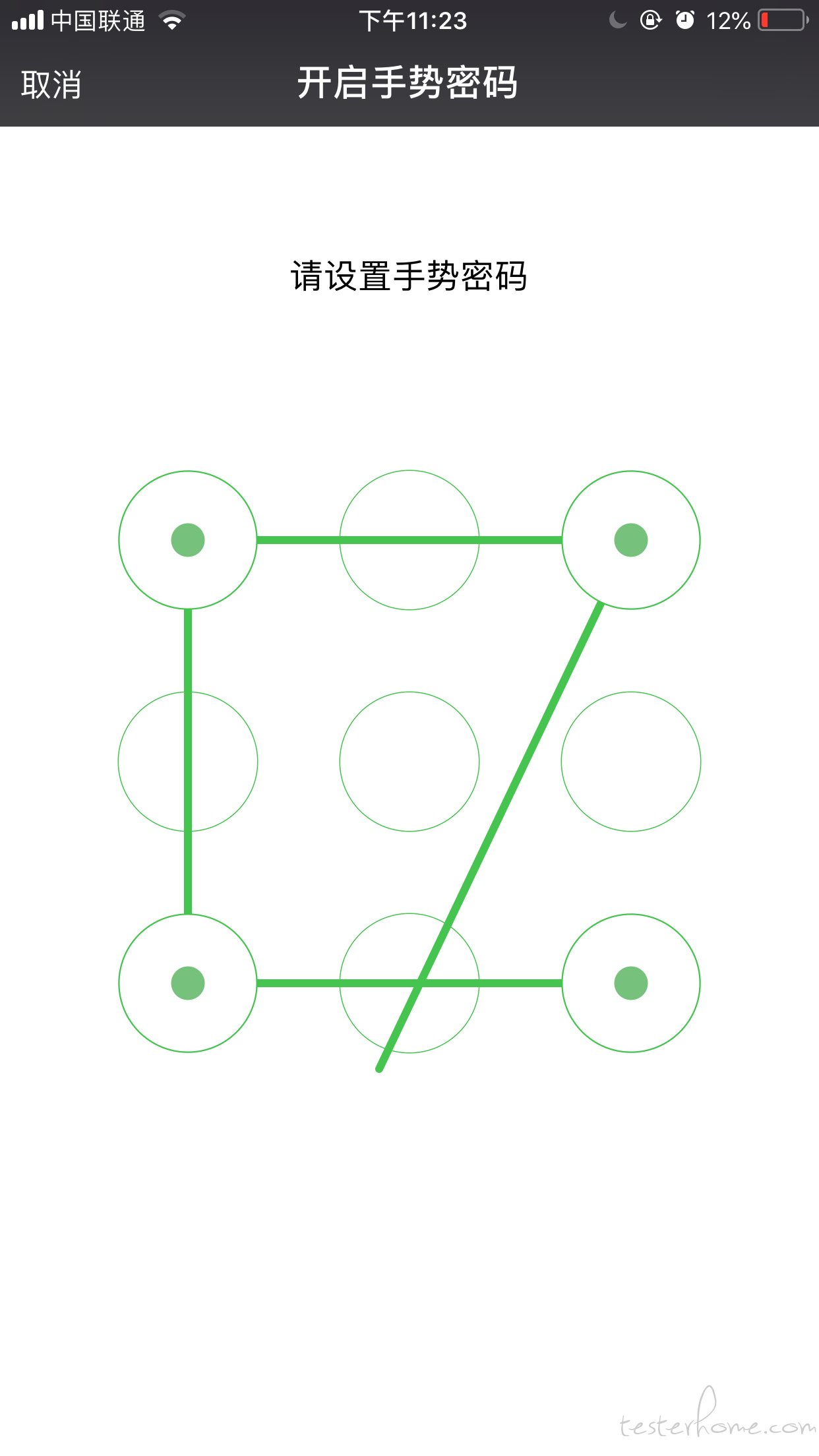
职业经验 某司面试题,输入任意一个数字 n,产生九宫格 n 位手势密码,例如输入 4,则产生的 (1,2,3,6)、(1,4,7,8) 都可以。九宫格规则是:数字只能连相邻的数字,且不能出现重复。请问使用 python 如何实现,谢谢。
某司面试题,输入任意一个数字 n,产生九宫格 n 位手势密码,例如输入 4,则产生的(1,2,3,6)、(1,4,7,8)都可以。九宫格规则是:数字只能连相邻的数字,且不能出现重复。请问使用 python 如何实现,谢谢。
import random
set([random.randint(1, 9) for i in n])
random.sample(range(1, 10), k=8)
这个题目意思是不是:1 到 9 数字中,输入 N,就从中选出 N 个数字?和九宫格没关系?
有关系的九宫格点过的数字不能再点,从他的描绘(例如输入 4,则产生的 (1,2,3,6)、(1,4,7,8) )应该是不能跳越进行设置密码
哈哈哈哈,我要是面试官对面答出 1 楼或者问出 2 楼的问题,在我心里已经是不过了
考的不是九宫格数字下一步能选的数字吗,随机出来一个 1239,你觉得九宫格能画得出来吗
我就觉得好奇,4 和 (1,2,3,6)、(1,4,7,8) 有什么关系先?没看出来
这道题粗暴一点的解法,先定义 1-9 数字,下一个可能出现的集合,比如{‘1’:【‘2’,‘4’,‘5’】},然后随机抽取加重复判断就好了
-。- 请澄清需求,(2,3,6,5,9,1 )是否符合
不太明白,为啥第二个数组的第一个值的坐标必须和第一个数组的最后那个值的坐标保持一致,比如说,第一组取了 1,2,那第二组开始取值,可以取 4 或者 6 啊,为啥一定要取 5
不考虑性能的,
1、直接 1-9 的 n 层循环,去除掉有重复数字的,然后生成一个 n 位数
2、生成一个 dict 数组,key 为 1-9 每个数字,value 是一个小的 dict 数组,该 dict 是 key 值无法直连的路径,比如 1 数字,1 数字直连到 3 必须经过 2,直连到 7 必须经过 4,直连到 9 必须经过 5,{1:{3:2, 7:4, 9:5}, 2:{8:5},...}
3、拿到第一步生成的 n 位数,对每一位进行判断,是否在 map 的 key 中,若在,该 key(例如为 a) 的下一步的值 (例如为 e) 是否在该 key 的 value(例如为 b) 中,若在 value 中,则判断这个 value 中的这个值 (例如为 c) 所对应的 value(例如为 d) 是否在 n 位数中的 e 所在位置的前面几位,若不在,则这个 n 为数不符合规则,反之,则符合规则
排列组合算法
我也思考了一下,思路如下:

假设密码最少两位 ,你确定(1,2,4)和(1,2,6)的九宫格连不起来吗
这题有点意思
瞎写了一个,不太明白九宫格能不能 1,2,1 这种。。 逻辑是只能去附近的那个值,不能越界
import random
def test(s, k, j, t):
if len(t) == 7:
return t
start = random.randint(0 if k - 1 < 0 else k-1, k if k + 1 > len(s)-1 else k + 1)
end = random.randint(0 if j - 1 < 0 else j-1, j if j + 1 > len(s[0])-1 else j + 1)
if s[start][end] in t:
return test(s, k, j, t)
t.append(s[start][end])
return test(s, start, end, t)
if __name__ == '__main__':
s = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
t = []
k = random.randint(0, len(s)-1)
j = random.randint(0, len(s[0])-1)
t = test(s, k, j, t)
print(t)
哈哈,我是根据实际情况来看的。你试下,大部分 app 或者手机手势密码都可以支持。从 9 到 1,因为中间的 5 已经选择了,所以其实会跳过。不过这样就更复杂了。
玩一下~~
from random import choice
def nine_demo(n):
if not 2<=n<=9 or not isinstance(n,int):
return " Invalid code"
d = list(range(1,10))
checker = [1,3,7,9]
result =[]
# 生成随机密码
for i in range(n):
code=choice(d)
result.append(code)
d.remove(code)
# 邻值越界检查
if i>=1 and code in checker and result[i-1] in checker:
result = []
return nine_demo(n)
return result
if __name__=='__main__':
for i in range(0,11):
print nine_demo(i)
1~9 通过 n/3 和 n%3 得到的值作为横纵坐标,然后任意一步的下一个可选数字需满足:
1、该数字没有被选过
2、该数字的坐标不在上个数字坐标的横纵坐标分别加或减 2 上
弱弱说一句,有手机的九宫格支持跳格的……所以这种还是问一句好……各位面试官也别一棒子就打死了……
我相信,大部分中级开发也写不出来。大家同意吗?
# -*- coding: utf-8 -*-
"""
主要实现思路
主要是根据手势密码锁来定义基本操作规则(只能连接临近的数字,不能越过数字进行连接),再运用类比法构造实现(不能出现重复的数字)。
"""
#定义基本规则
key=[[[1,2],[1,4],[1,5]],[[2,1],[2,3],[2,4],[2,5],[2,6]],[[3,2],[3,5],[3,6]],[[4,1],[4,2],[4,5],[4,7],[4,8]],[[5,1],[5,2],[5,3],[5,4],[5,6],[5,7],[5,8],[5,9]],[[6,3],[6,5],[6,8],[6,9],[6,2]],[[7,4],[7,5],[7,8]],[[8,7],[8,9],[8,4],[8,5,],[8,6]],[[9,6],[9,5],[9,8]]]
#1个
def rank1(key):
skey=[]
for i in range(1,10):
skey.append(key[i-1][0][0])
return skey
#2个
def rank2(key):
skey=[]
key1=rank1(key)
for key2 in key1:
for dkey in key[key2-1]:
skey.append(dkey)
return skey
#3个
def rank3(key):
skey=[]
key2=rank2(key)
for dkey in key2:
for key3 in key[dkey[-1]-1]:
tim=[]
if (key3[1] not in dkey) and (len(tim)<3):
for okey in dkey:
tim.append(okey)
tim.append(key3[1])
skey.append(tim)
return skey
#4个
def rank4(key):
skey=[]
key2=rank3(key)
for dkey in key2:
for key3 in key[dkey[-1]-1]:
tim=[]
if (key3[1] not in dkey) and (len(tim)<4):
for okey in dkey:
tim.append(okey)
tim.append(key3[1])
skey.append(tim)
return skey
#5个
def rank5(key):
skey=[]
key2=rank4(key)
for dkey in key2:
for key3 in key[dkey[-1]-1]:
tim=[]
if (key3[1] not in dkey) and (len(tim)<5):
for okey in dkey:
tim.append(okey)
tim.append(key3[1])
skey.append(tim)
return skey
#6个
def rank6(key):
skey=[]
key2=rank5(key)
for dkey in key2:
for key3 in key[dkey[-1]-1]:
tim=[]
if (key3[1] not in dkey) and (len(tim)<5):
for okey in dkey:
tim.append(okey)
tim.append(key3[1])
skey.append(tim)
return skey
#7个
def rank7(key):
skey=[]
key2=rank6(key)
for dkey in key2:
for key3 in key[dkey[-1]-1]:
tim=[]
if (key3[1] not in dkey) and (len(tim)<5):
for okey in dkey:
tim.append(okey)
tim.append(key3[1])
skey.append(tim)
return skey
#8个
def rank8(key):
skey=[]
key2=rank7(key)
for dkey in key2:
for key3 in key[dkey[-1]-1]:
tim=[]
if (key3[1] not in dkey) and (len(tim)<5):
for okey in dkey:
tim.append(okey)
tim.append(key3[1])
skey.append(tim)
return skey
#9个
def rank9(key):
skey=[]
key2=rank8(key)
for dkey in key2:
for key3 in key[dkey[-1]-1]:
tim=[]
if (key3[1] not in dkey) and (len(tim)<5):
for okey in dkey:
tim.append(okey)
tim.append(key3[1])
skey.append(tim)
return skey
print(rank4(key))
@show88118 我这么画不行?你是产品?你定需求?该问题并没有明确是否允许跳点连接好吧,所以就当个开放题,各种情况考虑的全面点,实际情况中,不明确的需求就跟产品技术进一步确认,产品说这里我不做限制,允许他跳点连接又怎么了!!!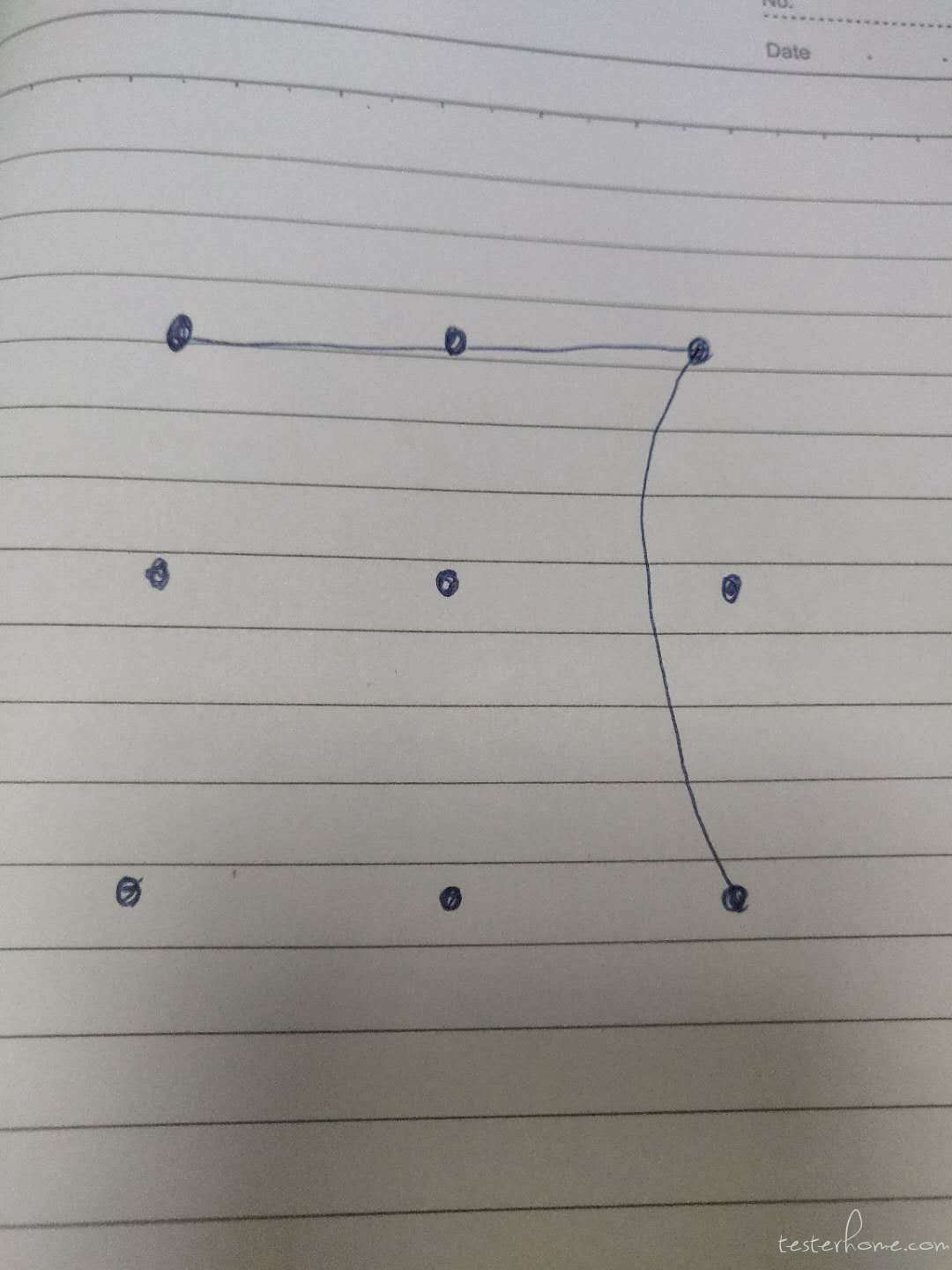
占个楼,下班的时候在公司写了一个,90 多 w 种情况,筛选出来应该是 30 多 w,笔记本还在跑。。估计要 5 个小时跑完,明天上午到公司贴答案。
def yy():
list1 = [(1, 3), (1, 6), (1, 7), (1, 8), (1, 9), (2, 7), (2, 8), (2, 9), (3, 1), (3, 4), (3, 7), (3, 8), (3, 9),
(4, 3), (4, 6), (4, 9), (6, 1), (6, 4), (6, 7), (7, 1), (7, 2), (7, 3), (7, 6), (7, 9), (8, 1), (8, 2),
(8, 3), (9, 1), (9, 2), (9, 3), (9, 4), (9, 7)]
l = []
m = []
s = 0
for y in range(10):
if y == 0:
pass
else:
l.append(y)
for u in range(9):
m.extend((list(permutations(l, u+1))))
print(len(m))
for i in list1:
for n in m[:]:
if i.__str__().strip('()') in n.__str__().strip('()'):
m.remove(n)
s += 1
print(s)
else:
pass
return len(m)
print(yy())
算出来的答案,用的穷举法,算的比较慢,讲下思路,Android 九宫格最少要 4 位,题目应该是 1-3 位数也应该要满足,我先得到 9 个数字的 1-9 的所有组合排列,剔除不符合规则的跳跃方式,通过穷举,一个个对比,90 多 w 条数据符不符合规则。重新计算一遍,9w 多不对,漏了一个指针的问题,晚点贴。
参考知乎答案:手机的九宫格图案解锁总共能绘出多少种图案? - linkwun 的回答 - 知乎
impossible = {13: 2,
46: 5,
79: 8,
17: 4,
28: 5,
39: 6,
19: 5,
37: 5,
31: 2,
64: 5,
97: 8,
71: 4,
82: 5,
93: 6,
91: 5,
73: 5,
}
def func(n):
if not 1 <= n <= 9:
raise ValueError("1 <= n <= 9")
numbers = list(range(1, 10))
result = []
num = random.choice(numbers)
result.append(num)
numbers.remove(num)
for i in range(n-1):
next_numbers = numbers[:]
for next_num in next_numbers[:]:
key = result[-1]*10 + next_num
if key in impossible:
if impossible[key] not in result:
next_numbers.remove(next_num)
num = random.choice(next_numbers)
result.append(num)
numbers.remove(num)
return result
发现一个问题:
1、不同厂商对此处理并不相同,华为手机屏幕解锁在一条直线上三点(如 1、5、9),选择起点、终点后中间那个点会自动连接起来。
2、某些 APP 解锁可以直接绕弯连接起点、终点。
微信钱包:
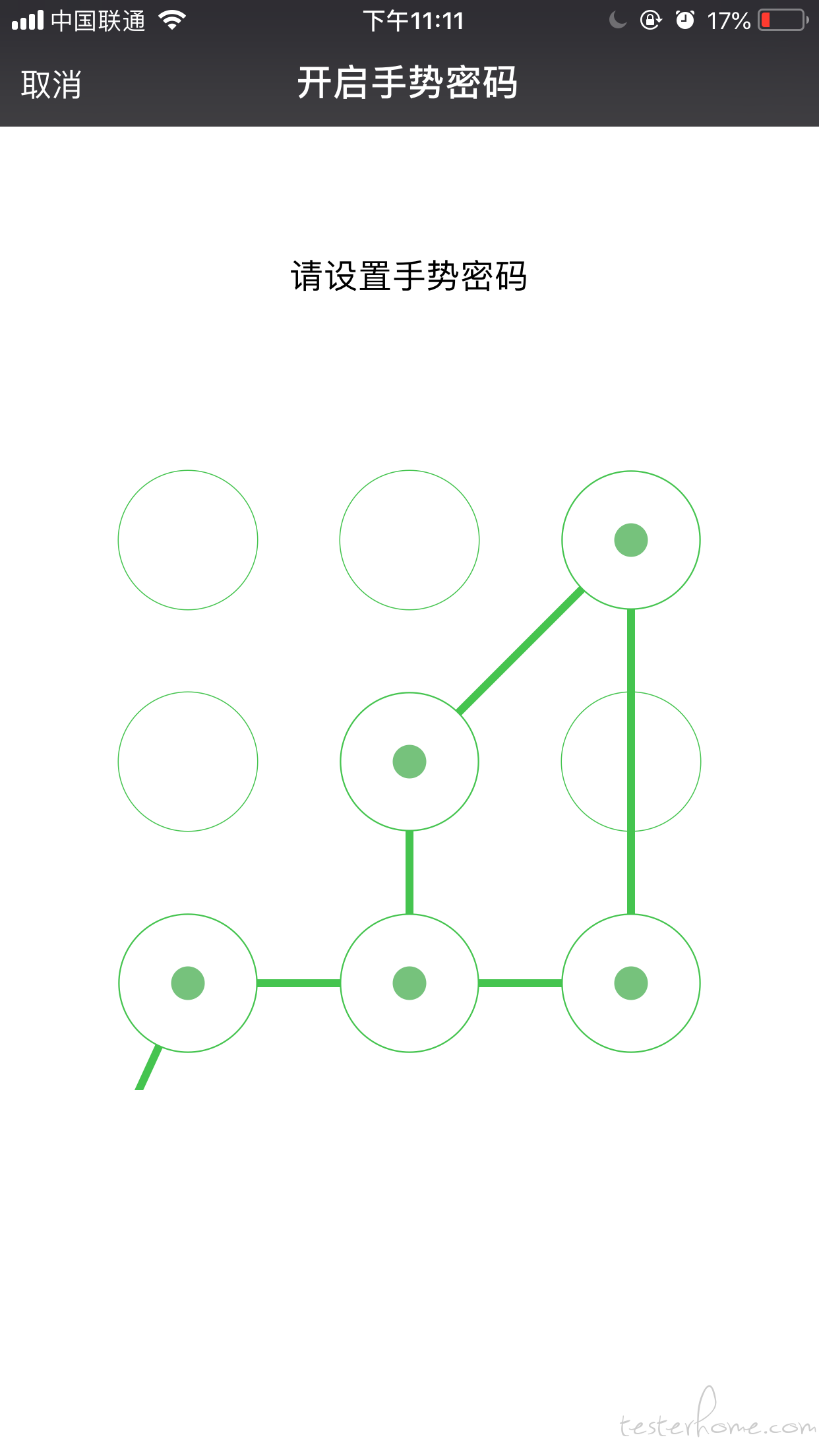
京东金融:

下次还得与面试官确认一下需求。
喜欢一个排列组合简单的答案:从 1 到 9 随机有序选择 n 个数字(n>=2&&n<=9),例如选择 4 个点的结果为:
4
A 9 =9*8*7*6
结果正确。。思路不清楚?这个逻辑我有点没明白。
你说要求高,对性能有要求还另说。。。面试的短短时间里,写出一个有点难度的算法题,还要求性能?敢问是什么公司?招什么岗?
嗯,我想这里面试官都没有跟你明确规则,我也查了下,九宫格连点锁屏也没有一套严格的统一的公开的,所有人必须严格按照这套去执行的规则,或者说大家心里默认的那套规则也没有,那么所有的执行,就不应该靠自己的臆想,瞎想,你说什么就是什么,这套规则的制定者就是各司的产品,需求跟着产品走。
写了好久,我把所有情况都给写出来了,额!!!!!
def relist(no):
if no==1:
return [2,4]
if no==2:
return [1,3,5]
if no==3:
return [2,6]
if no==4:
return [1,5,7]
if no==5:
return [2,4,6,8]
if no==6:
return [3,5,9]
if no==7:
return [4,8]
if no==8:
return [5,7,9]
if no==9:
return [6,8]
def result_ok(list,n):
result = []
for x in list:
if n-1>0:
items=result_ok(relist(x),n-1)
for item in items:
if type(item)==list:
item.insert(0,x)
result.append(item)
if type(item)==int:
result.append([x, item])
else:
item.insert(0, x)
result.append(item)
else:
return list
return result
if __name__=='__main__':
list=[1,2,3,4,5,6,7,8,9]
result=result_ok(list,9)
l=[]
for its in result:
leg=0
for a in its:
if its.count(a)>1:
leg=1
if leg==0:
l.append(its)
print(l)
a=[[1,2,3],[4,5,6],[7,8,9]],有穷遍历 a[i][j] 的邻边可破。
import random
def getCanSelect(n,address,isSelectAddress):
initNumX=address[0]
initNumY=address[1]
canBeSelect=[]
if n>0:
for x in range(initNumX-1,initNumX+2):
if x<3 and x>-1:
for y in range(initNumY-1,initNumY+2):
if y<3 and y>-1:
if abs(initNumX-x)+abs(initNumY-y)<3:
if initNumX==x and initNumY==y:
continue
newaddRess=[x,y]
if isSelectAddress.count(newaddRess)==0:
canBeSelect.append(newaddRess)
while True:
if len(canBeSelect)>0:
indexNum=random.randint(0,len(canBeSelect)-1)
nextAddress=canBeSelect[indexNum]
isSelectAddress.append(nextAddress)
else:
raise Exception
try:
getCanSelect(n-1,nextAddress,isSelectAddress)
except Exception as e:
#如果出现异常说明节点选择不对,需要重新选择
canBeSelect.remove(nextAddress)
isSelectAddress.pop()
continue
break
def selectNum(n):
nodeMap={1:[0,0],2:[0,1],3:[0,2],4:[1,0],5:[1,1],6:[1,2],7:[2,0],8:[2,1],9:[2,2]}
node=[[1,2,3],[4,5,6],[7,8,9]]
isSelectAddress=[]
initNum=random.randint(1,9)
address=nodeMap.get(initNum)
isSelectNum=[]
isSelectAddress.append(address)
getCanSelect(n-1,address,isSelectAddress)
for index in isSelectAddress:
x=index[0]
y=index[1]
isSelectNum.append(node[x][y])
return tuple(isSelectNum)
print(selectNum(9))
妈蛋,写了 2 小时,还不知道是不是真的都考虑到了,面试要求这么细的话,铁定挂了
我的意思是面试出这么难的题,可能是他们公司要求高。就算求职者给了一个正确结果,以面试官的特点他也可能认为性能没有达到要求(除非公司技术领导、hr 定的要求必须了解算法)
产品需求:向左
技术实现:向右
产品需求:向前
技术实现:向后
你对产品说:我不听我不听,你们是谁啊,你们又不是上帝,我凭什么听你的啊?
你对技术说:来 ,我们把所有情况都实现一遍。
我就是这个逻辑的。。。你写的是 1 个密码几种,2 个密码几种,3 个密码几种,一直列举到 9 种。
我是列出 9 种数字所有的组合排列,剔除中间不符合规则的。1 不可以连 3,6,7,8,9。2 不可以连 7,8,9,3 不可以连 1,4,7,8,9 等等。
得到的最后所有的组合。
嗯 不过我那个输出 print(rank4(key)) 就是列出当前密码组合,输出 print(len(rank4(key))) 就是当前密码组合有多少种。
import random
ruledict = {"1":"2,4",
"2":"1,3,5",
"3":"2,6",
"4":"1,5,7",
"5":"2,4,6,8",
"6":"3,5,9",
"7":"4,8",
"8":"5,7,9",
"9":"6,8"
}
def get_number_from_ruledict(n):
# -1 value error
# -2 type error
if type(n) == int :
if n>=1 and n <= 9:
pass
else:
return -1
else:
return -2
#str to int
the_number_dict_int = {}
the_number_str = ruledict[str(n)]
the_number_dict_str = the_number_str.split(',')
length = len(the_number_dict_str)
for i in range (length):
the_number_dict_int[i]=the_number_dict_str[i]
result = the_number_dict_int[random.randint(0,length-1)]
return int(result)
def randx(n):
# -1 value error
# -2 type error
if type(n) == int :
if n>=1 and n <= 9:
pass
else:
return -1
else:
return -2
#keep the sequence
number_sequence = []
the_last_number=random.randint(1,9)
number_sequence.append(the_last_number)
for i in range(n-1):
next_number = get_number_from_ruledict(the_last_number)
#check
while( next_number in number_sequence):
next_number = get_number_from_ruledict(the_last_number)
number_sequence.append(next_number)
#update
the_last_number = next_number
return number_sequence
randx(9)
想的很简单,没有遍历,如果有其他需求,再更改,在这套设计里,1,5,9 是不相邻的,有点像华容道小游戏的那样,规定为十字相邻
import random
def getCloseNumList(num):
locList = dict(enumerate(map(lambda x:((x-1)/3,(x-1)%3),range(1,10)), 1))
num_x, num_y = locList.get(num)
ret = []
for j in locList:
if j!=num:
j_x,j_y = locList.get(j)
if abs(j_x-num_x)<=1 and abs(j_y-num_y)<=1:
ret.append(j)
return ret
def run(times):
try:
result = []
for i in range(times):
if i == 0:
last = random.choice(range(1, 10))
result.append(last)
else:
choiceList = list(set(getCloseNumList(last)) - set(result))
last = random.choice(choiceList)
result.append(last)
return result
except:
run(times)
def loadTest(): #新增性能测试
start = time.time()
for i in xrange(10000):
run(2)
print "100000次2 : %f" % (time.time() - start)
start = time.time()
for i in xrange(10000):
run(5)
print "10000次5 : %f" % (time.time() - start)
start = time.time()
for i in xrange(5000):
run(7)
print "5000次7 : %f" % (time.time() - start)
try:
start = time.time()
for i in xrange(2000):
run(8)
print "2000次8 : %f" % (time.time() - start)
except Exception, e:
print "2000次8 : 运行异常:%s" % (e.message)
try:
start = time.time()
for i in xrange(1000):
run(9)
print "1000次9 : %f" % (time.time() - start)
except Exception, e:
print "1000次9 : 运行异常:%s" % (e.message)
if __name__ == '__main__':
times = raw_input("请输入节点数量:")
if not times.isdigit() or int(times)>9 or int(times)<1:
print "无效数字!"
exit(1)
print run(int(times))
loadTest()
性能测试结果:

手机九宫格,请拿出来能这么连线的手机,另外考察点应该得是大部分九宫格都 ok,你拿一个极稀少的 case 去解释,如果我是考官的话我不接受
这里我不想多说了,我的观点表达的很明确,有异议提出来,进一步跟相应的人确认下结果,而不是你刚开始说的那样,“随机出来一个 1239,你觉得九宫格能画得出来吗”,这也只是你的个人观点,觉得不能连,例子 36 楼已经给出来,即使没给出来,也不应该因为这种情况少就不去考虑,我举个极稀少的 case 去反驳你,也不代表我就赞同,就支持跳格连接。
你考虑可以跳格没问题,考题不是投机,你说的跳格情况我认为有,如果考官(产品)允许跳格,那么随机算对,不跳格的方案也算对,如果不允许,随机算错,不跳格的方案还是对。所以我所说的不觉得过的原因,要么你问我,九宫格的理解,要么你写出一个全部兼容的方案。
我用了个递归函数,然后把所有情况罗列出来,然后去重,结果就是了,在第 48 楼。罗列出 N 个数字的所有情况。代码丑陋不堪,见谅!
没懂这题目是啥意思?假如我输入 10 咋办?
这个题挺有意思呢,动动脑筋吧。
也许我对九宫格的选取节点的功能不了解,或者自己给自己找茬,我是想说节点选择后不能再选,如此我考虑一个回退的问题:如果前提是不能跳选的话,当节点数是 5 及以上的时候,可能会出现没有节点可选的情况,比方说 4,5,8,7 这个时候第 5 个节点没法再选了,所以需要回退到 8 这个节点,同时把 8 节点当前可选的节点中去掉 7 节点,然后再随机选择节点。直到选择到足够数量的节点为止。
@george.he 看看这个,我真的消耗了挺多脑细胞,不过最终是做好了。。
默认 5 位,-l 指定位数
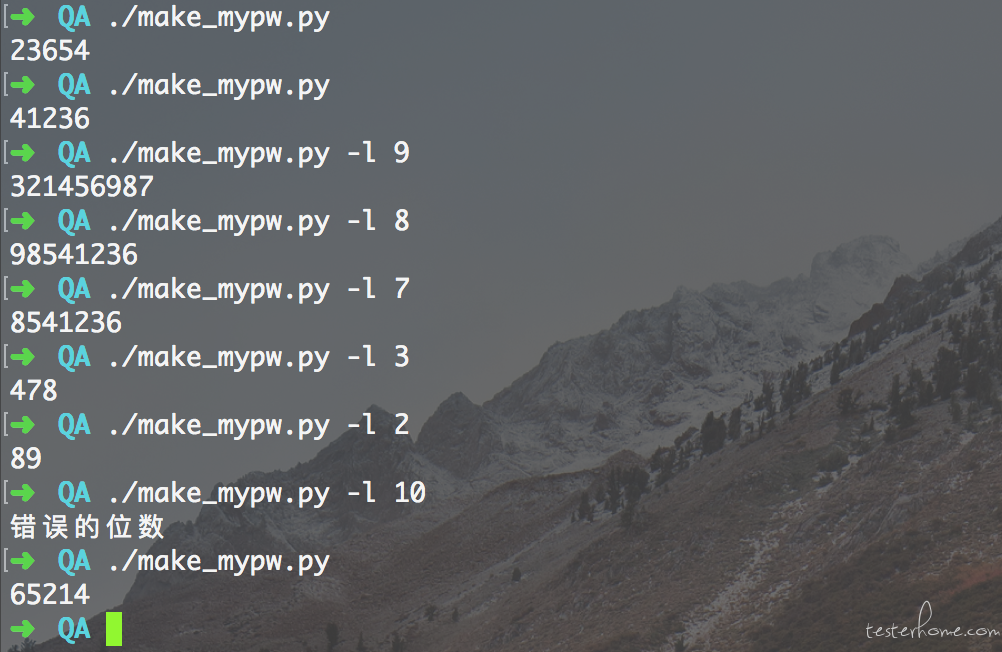
#!/usr/bin/env python3
"""
输入位数(1-9),生成9宫格密码,要求
1. 数字只能相邻
2. 不可重复
思路:
正向推导时,有可能随机取数时因重复导致重算,所以考虑:
1. 算出1-9位的所有可用密码
2. 输入位数后从对应的密码中随机返回一个
"""
import random
import argparse
# 每个数字和可用的相邻数字,分"可走对角"和"不走对角"两种方式
# 不走对角使用:
# base_dict = {1: [2, 4], 2: [1, 3, 5], 3: [2, 6], 4: [1, 5, 7], 5: [2, 4, 6, 8],
# 6: [3, 5, 9], 7: [4, 8], 8: [5, 7, 9], 9: [6, 8]}
# 可走对角使用:
base_dict = {1: [2, 4, 5], 2: [1, 3, 4, 5, 6], 3: [2, 5, 6], 4: [1, 2, 5, 7, 8], 5: [1, 2, 3, 4, 6, 7, 8, 9],
6: [2, 3, 5, 8, 9], 7: [4, 5, 8], 8: [4, 5, 6, 7, 9], 9: [5, 6, 8]}
def parse_args():
p = argparse.ArgumentParser()
p.add_argument('-l', '--long', type=int, default=5, help="定义密码长度")
return p.parse_args()
def make_one():
"""
1位密码就是1-9随机选一个数
"""
pw = [[i] for i in range(1, 10)]
return pw
def make_more(pre_pw):
"""
2位和以上的密码,依赖前一次生成的密码,最后一位相邻的所有组合
然后排重
"""
pw_dup = []
for i in pre_pw:
for j in base_dict[i[-1]]:
temp = i[:]
temp.append(j)
pw_dup.append(temp)
pw = [i for i in pw_dup if len(set(i)) == len(i)] # 去重
return pw
def make_all_pw():
"""
循环将生成所有位数的密码并存为dict
"""
all_pw = dict()
all_pw[1] = make_one()
for i in range(2, 10):
all_pw[i] = make_more(all_pw[i-1])
return all_pw
def main():
args = parse_args()
pw_l = args.long
if 0 < pw_l < 10:
my_all_pw = make_all_pw()
my_pw = random.choice(my_all_pw[pw_l])
print("".join(str(i) for i in my_pw))
else:
print("错误的位数")
if __name__ == '__main__':
main()
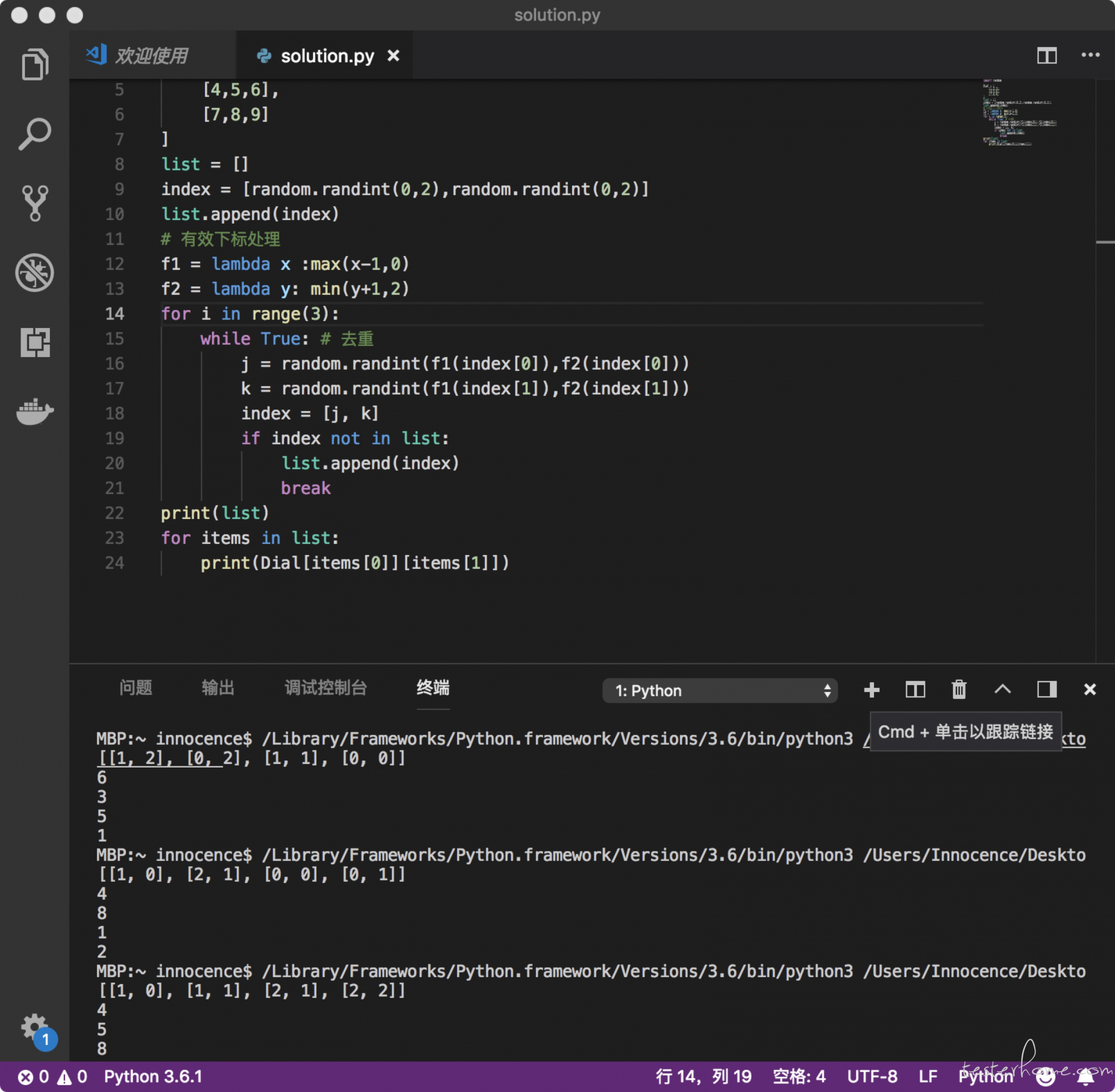
直接操作号码盘下标可行~~代码生疏了生疏了
更新一波:产生重复的时候忘记恢复 index
import random
Dial = [
[1,2,3],
[4,5,6],
[7,8,9]
]
list = []
index = [random.randint(0,2),random.randint(0,2)]
list.append(index)
# 有效下标处理
f1 = lambda x :max(x-1,0)
f2 = lambda y: min(y+1,2)
for i in range(3):
while True: # 去重
j = random.randint(f1(index[0]),f2(index[0]))
k = random.randint(f1(index[1]),f2(index[1]))
index = [j, k]
if index not in list:
list.append(index)
break
else:
index = list[-1]
print(list)
for items in list:
print(Dial[items[0]][items[1]])
哦哦,你理解的规则立对角不相邻啊,我理解的相邻对角也是可行的 比如 15 35
不过这个 4812 感觉真的是有 bug。。。。。自测跑了十几遍觉得没问题才发上来的
随后检查了下,修复了这个 bug
李姐万岁~
讲下思路
假设给出的列表都是规范的 A*A 的格式,如 1-9 三行行列,1-16 四行四列,那么大致可以把数字分为三类 (g 为长度开平方,因为前提条件,g 必定为自然数):
-
固定的角落,有四个数值,左上:1,右下:g, 左下:1+g*(g-1), 右上: g
- 左上-1,右下 +1 超出边界
- 左下 +g,右上-g 超出边界
-
四边除角落外的值,这类值,因为数值间的关系上下对称,左右对称,是可以遍历两次得到的
- +g 或者-g 超出边界,那肯定是第一或者最后一行的数字了,反之则是第一或最后一列的数字
- 值小于 g(也就是第一行最后一个数字),那肯定是第一行的数了,反之是最后一行的数
- 值如果刚好是 g 的倍数关系,那肯定是在右侧了,反之则是左侧边界
剩下的就是处于中间的值
而以上三种类型,可以写三个方法定义,每一种都有特定的规律来取值,这里没说不能斜着,因此我将斜着临近的数也算进去了。
实现代码(基于 python3.6)
# coding:utf8
# author: ryan
import random
from math import sqrt
list_a = [1,2,3,4,5,6,7,8,9]
L = len(list_a)
# 每一行个数
g = int(sqrt(L) )
# 四个角
corner_list = [1,g,1+2*g,L]
# 除角落外的边界数字
middle_list = []
for i in range(2,g):
# 首行
middle_list.append(i)
# 末行
middle_list.append(i+2*g)
for i in range(1+g,1+2*g,g):
# 左侧
middle_list.append(i)
# 右侧
middle_list.append(i+g-1)
# 角落数字推算下一个数
def corner_make_nextnum(x):
temp_list =[]
# 边角数字固定只有四个,分两种, 1 和最大值 (也就是L))往前-1或者往后+1,不在1到L之间间,是一类。 另外两个是另一类
if x-1 not in list_a or x+1 not in list_a:
# 1 和 len, x-1不在list_a里,是左上角,反之是右下角
if x-1 not in list_a:
# 左上角,符合数字,右,下,右下
x_right = x + 1
x_down = x + g
x_right_down = x + g + 1
temp_list.append(x_right)
temp_list.append(x_down)
temp_list.append(x_right_down)
else:
# 右下角,符合数字,左,上,左上
x_left = x - 1
x_up = x - g
x_left_up = x - g - 1
temp_list.append(x_left)
temp_list.append(x_up)
temp_list.append(x_left_up)
else:
# 如果x-g还在list_a里,是左下角,反之是右上角
if x-g in list_a:
# 左下角,符合数字:上,右上,右
x_up = x - g
x_right_down = x - g + 1
x_right = x + 1
temp_list.append(x_up)
temp_list.append(x_right_down)
temp_list.append(x_right)
else:
# 右上角,符合数字:左,左下,下
x_left = x - 1
x_left_down = x + g - 1
x_down = x + g
temp_list.append(x_left)
temp_list.append(x_left_down)
temp_list.append(x_down)
next_num = random.choice(temp_list)
return next_num
# 每行中间数推算下一个数
def line_without_corner(x):
temp_list = []
# 如果+g,-g不在list_a中,那就是横向的
if x+g not in list_a or x-g not in list_a:
x_left = x - 1
x_right = x + 1
# 如果x比g小,那说明是第一行的,反之是最后一行的
if x < g:
# 第一行符合数字为左,右,下,临近的左下,右下
x_down = x + g
x_left_down = x + g - 1
x_right_down = x + g + 1
temp_list.append(x_down)
temp_list.append(x_left_down)
temp_list.append(x_right_down)
else:
# 最后一行符合数字为左,右,上,临近的左上,右上
x_up= x - g
x_left_up = x - g - 1
x_right_up = x - g + 1
temp_list.append(x_up)
temp_list.append(x_left_up)
temp_list.append(x_right_up)
temp_list.append(x_left)
temp_list.append(x_right)
# 纵向的,且如果是g的倍数,则表示是在右侧边界,若不是则表示在左侧边界
else:
# 自然数,横竖个数相同的这种排列,上下相差始终为g
x_up = x - g
x_down = x + g
# 右侧边界,可以除了上下还有临近的左侧,左上,左下
if x%g == 0:
x_left = x - 1
x_left_up = x - g - 1
x_left_dwwn = x + g - 1
temp_list.append(x_left)
temp_list.append(x_left_up)
temp_list.append(x_left_dwwn)
# 左侧边界,可以除了上下还有右临近的右侧,右上,右下
else:
x_right = x + 1
x_right_up = x - g + 1
x_right_dwwn = x + g + 1
temp_list.append(x_right)
temp_list.append(x_right_up)
temp_list.append(x_right_dwwn)
temp_list.append(x_up)
temp_list.append(x_down)
next_num = random.choice(temp_list)
return next_num
# 中间的数字推算下一个数,上,下,左,右,左上,左下,右上,右上,固定有8个
def middle_make_nextnum(x):
temp_list = [x-1, x+1, x-g, x+g, x-g-1, x-g+1, x+g-1, x+g+1]
next_num = random.choice(temp_list)
return next_num
# 根据已有数字推测下一可能数字
def available_next(x):
if x in corner_list:
next_number = corner_make_nextnum(x)
elif x in middle_list:
next_number = line_without_corner(x)
else:
next_number = middle_make_nextnum(x)
return next_number
def random_make_num(n):
first_num = random.choice(list_a)
passwd_list = [first_num]
i = 1
while i < n:
next_num = available_next(first_num)
# 过滤重复值
if next_num in passwd_list:
pass
else:
passwd_list.append(next_num)
first_num = next_num
i+=1
return passwd_list
if __name__ == "__main__":
passwd_list = random_make_num(4)
print(passwd_list)
运行一下啊,[8, 6, 4, 5],[8, 9, 6, 4],[4, 5, 7, 2]
试着算个 8 位的,[5, 2, 8, 7, 4, 9, 1, 6],[5, 9, 1, 8, 2, 7, 6, 3]
或者,亲自算一个 9 位的试试?
已修复
在过滤重复值的时候,判断下一跳,没有把前一跳作为参数传到 available_nex() 方法去,一直用的初始的 first_num。
9 位密码能推导出来真得靠运气啊。。。
你正向推导,万一推不出来呢,例如:5-6-8-9---就卡住了,重来,3-5-9-6---又卡住了。。。
想了半天,越想越复杂,当 n 比较大的时候,且已有数字可以横着或者竖着或者斜着把这个方形切割。
那么 n<2g
那么 n>2g 的时候,情况就比较复杂了,截面产生后,落点只能去往截后数字多的那块区域,但进入这里面找落点还得遵循规则,还可以再产生截面。。。
单纯的 9 宫格,大不了可以写死,而想要写一个通用性的方法,托大了。
先留着,想到方案再接上。
使用我的方法,修改 base_dict = {1: [2, 4, 5], 2: [1, 3, 4, 5, 6], 3: [2, 5, 6], 4: [1, 2, 5, 7, 8], 5: [1, 2, 3, 4, 6, 7, 8, 9],
6: [2, 3, 5, 8, 9], 7: [4, 5, 8], 8: [4, 5, 6, 7, 9], 9: [5, 6, 8]} ,把斜对角加上就可以了。。。
所有可用的密码有 10305,比不加斜对角的大了很多,所以计算稍微慢一些~
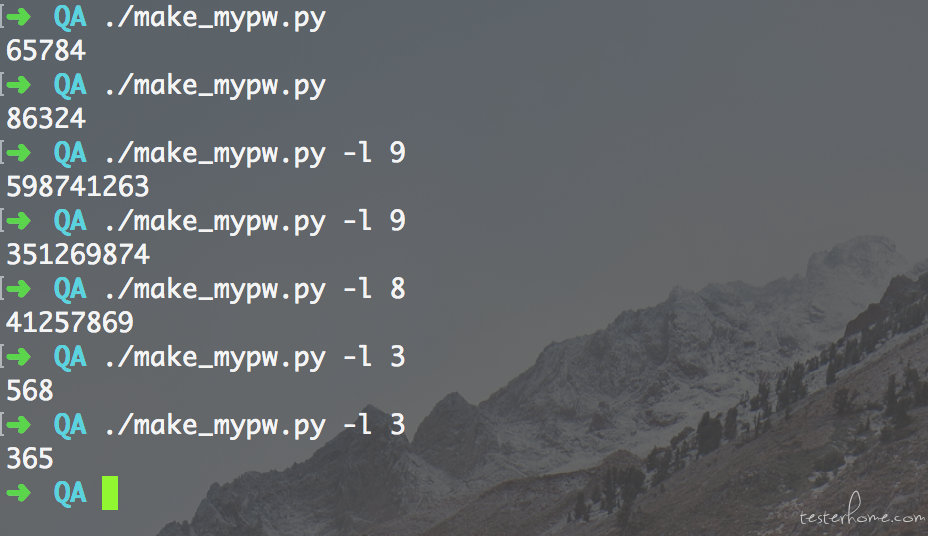
排除法最简单
1、定义 base_dict = {1: [2, 4, 5], 2: [1, 3, 4, 5, 6], 3: [2, 5, 6], 4: [1, 2, 5, 7, 8], 5: [1, 2, 3, 4, 6, 7, 8, 9],
6: [2, 3, 5, 8, 9], 7: [4, 5, 8], 8: [4, 5, 6, 7, 9], 9: [5, 6, 8]}
2、递归获取 n 位密码。递归思路:n-1 位密码的列表逐个判断是否可以再加 1 位,如果是则加 1 位变为新的 n 位密码放到 n 位密码列表;当 n-1 = 1 时,返回 [[1], [2], [3], [4], [5], [6], [7], [8], [9]]
3、如何判断一个密码列表是否可以再加 1 位:全集 [1, 2, 3, 4, 5, 6, 7, 8, 9] 去掉当前密码已经使用的数字,与 base_dict[当前密码最后一位] 交集,如果交集长度大于 0,则可以再加 1 位
以上基于 python3.6 实现,效率还是可以的
def run():
pw = PassWd(9)
print(pw.passwd())
class PassWd:
def __init__(self, n):
# self.start = random.randint(1, 9)
self.n = n
self.all = [1, 2, 3, 4, 5, 6, 7, 8, 9]
self.besides = {1: [2, 4, 5], 2: [1, 3, 4, 5, 6], 3: [2, 5, 6],
4: [1, 2, 5, 7, 8], 5: [1, 2, 3, 4, 6, 7, 8, 9],
6: [2, 3, 5, 8, 9], 7: [4, 5, 8], 8: [4, 5, 6, 7, 9],
9: [5, 6, 8]}
def passwd(self):
print('n:%d' % self.n)
res = self.generate_passwds(self.n)
print('pwds_count:%d, pws:%s' % (len(res), res))
return res[random.randint(0, len(res)-1)]
def generate_passwds(self, count):
if count == 1:
return [[1], [2], [3], [4], [5], [6], [7], [8], [9]]
new_res = []
res = self.generate_passwds(count - 1)
for pwd in res:
numbers = self.next_numbers(pwd)
if numbers:
for child in numbers:
new_res.append(pwd + [child])
return new_res
def next_numbers(self, pwd):
numbers = list(set(self.all).difference(set(pwd)).intersection(set(self.besides[pwd[-1]])))
return numbers
做过,两种写法,胸弟是 jianglin 吗?
提供一种思路,空间换时间,运行效率挺高的
# -*-coding=utf-8-*-
import random,time,sys
sys.setrecursionlimit(10**9)
a = [1, 2, 3, 4, 5, 6, 7, 8, 9]
a1 = [2, 5, 4]
a2 = [1, 3, 4, 5, 6]
a3 = [2, 5, 6]
a4 = [1, 2, 5, 7, 8]
a5 = [1, 2, 3, 4, 5, 6, 7, 8, 9]
a6 = [2, 3, 5, 8, 9]
a7 = [4, 5, 8]
a8 = [4, 5, 6, 7, 9]
a9 = [5, 6, 8]
def makeNum(n):
t = random.choice(a)
result = [t]
for i in range(n-1):
if list(set(globals()['a' + str(t)]) - set(result)):
t = random.choice(list(set(globals()['a' + str(t)]) - set(result)))
result.append(t)
else:
return makeNum(n)
return result
这种先把每个能连接的数字对打出来,这样就弄了一个有向图(每个数字有一堆 children 可以连)
然后就随机选 k 次就好了,用个 set 记录走过的路径,注意有时候生成长度不够要回溯
#/str/bin/python
#coding=utf-8
output = []
list1 = [2,4,5]
list2 = [1,3,4,5,6]
list3 = [2,5,6]
list4 = [1,2,5,7,8]
list5 = [1,2,3,4,6,7,8,9]
list6 = [3,2,5,8,9]
list7 = [4,5,8]
list8 = [7,4,5,6,9]
list9 = [8,5,6]
dict = {}
dict[1]=list1
dict[2]=list2
dict[3]=list3
dict[4]=list4
dict[5]=list5
dict[6]=list6
dict[7]=list7
dict[8]=list8
dict[9]=list9
output = [0,0,0,0]
for num1 in range(1,9):#123456789
output[0]=num1#1
for num2 in dict[num1]:#num2 in 2 4 5
output[1]=num2#1 2
for num3 in dict[num2]:#num3 in 1 3 4 5 6
if num3 == output[0]:
continue
else:
output[2]=num3#1 2 3
for num4 in dict[num3]:#num4 in 2 5 6
if num4 == output[1] or num4 == output[0]:
continue
else:
output[3]=num4#1 2 3 5
print(output)
这个题考的是有向图和广度优先搜索吧
from collections import deque
import random
graph = {}
graph[1] = [2, 4]
graph[2] = [1, 3, 5]
graph[3] = [2, 6]
graph[4] = [1, 5, 7]
graph[5] = [2, 6, 8, 4]
graph[6] = [3, 9, 5]
graph[7] = [4, 8]
graph[8] = [5, 9, 7]
graph[9] = [6, 8]
def gen(n, start=1):
"""
创建一个图,保存其与周围节点的关系
创建一个队列,用于保存待check节点
创建一个列表,用于保存已经check过的节点
当队列不为空时,且步数小于n(可以理解为需要多少个节点就是走多少步)
求出没有check过的节点,然后从中随机选一个节点,直到队列为空
最后,如果所得结果小于n,说明没有满足n个节点的结果,否则返回正确结果
:param n: 节点个数
:param start: 开始节点
:return:
"""
q = deque()
q.append(start)
already = []
step = 0
res = []
while q:
data = q.popleft()
if step < n:
res.append(data)
already.append(data)
g = [x for x in graph[data] if x not in already]
if g: q.append(random.choice(g))
step += 1
if len(res) < n: return False
return res
深度优先 广度优先 了解下