从 L8-L9 主要是介绍贪心算法。

活动选择问题

问题定义：
input:A={(x1,y1),(x2,y2),....} xi<yi
output S<=A non-overlapping max|S|
这里是求可以选择活动的最大数目，不是最长时间，这里依靠贪心就可以完成。
迭代选择最先结束的活动
算法导论 (原书第三版) 中的 P239 页介绍。

Set Cover

问题定义：现在有一个集合 A，其中包含了 m 个元素（注意，集合是无序的，并且包含的元素也是不相同的），现在 n 个集合，分别为 B1、B2、...、Bn。并且这 n 个集合的并集恰好等于 A 集合，即：B1UB2UB3U...UBn=A。
是否存在 B 集合的最小子集，且他们的并集也等于 A 集合？
贪心算法：

设定最优化的最小子集为 J* 可以证明：
|J*|<=|J|<=|J*|loge|U|
证明方式：
n(t+1)<=nt-nt/|J*|

MST(最小生成树)

对于 G=(V,E)
引论 1：最小生成树是（a）无环的（b）|E(G')| = |V|-1

引论 2：设边集 X 是 G=(V,E) 的某个最小生成树的一部分。选定任一节点集合 S 属于 V，使得 X 中没有跨越 S 合 V-S 的边，若 e 是跨越 S 和 V-S 的权重最轻的边，则 X U {e}也是某个 MST 的一部分。

Kruskal 算法

关于 find（路径压缩）和 Union 的方法 CS61B 中提过。

L10-L11 的前半部分，继续介绍 MST

L10

L10 主要介绍的是交并集的相关算法。
核心算法是 Disjoint-set Forest.

路径压缩

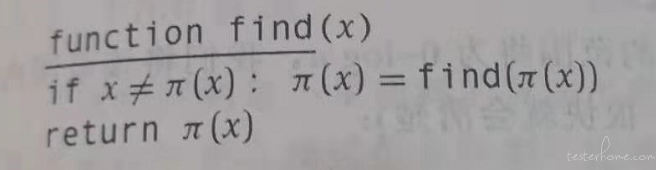
花了大量的篇幅推理 runtime 是 O((m+n) log*n)
先证明了三个引理：
1.任意一个根节点为 k 的树至少包含 2^k 个节点
2.ranks 只会严格 +1
3.rank 为 k 的节点数<= n/2^k

证明是通过将 ranks 分组为：
[0,1),[1,2),[2,2² ),[2² ,2²² ),[k,2^k)
具体的证明请参考算法概论的 P153.
算法导论的证明过于复杂。（完全没看明白）

L11 前半部分介绍了 Prim 算法
运算时间：基于 binary heaps 是 O(mlgn)
基于 Fibrocci heaps 的是 O(m+nlogn)
CS170 没有介绍 Fibrocci heap。