Lesson 2.5 Distributed Memory Sorting

Bitonic Merge via Transposes

Bitonic Sort 的正常并行方式如上图所示。
两个算法的 Communication time 相同。
Communication time = (α + (b (β/p)) log(p))

对于一个 N=16,P=4 的情况
用 Cyclic scheme 的前半段 +Full Connect+Block distribution scheme 的后半段进行拼接。
在这种情况下，跨 P 的交互只有 Full Connect。
对应的 Communication time =α (P-1)+ β (n/P)((P-1)/P)

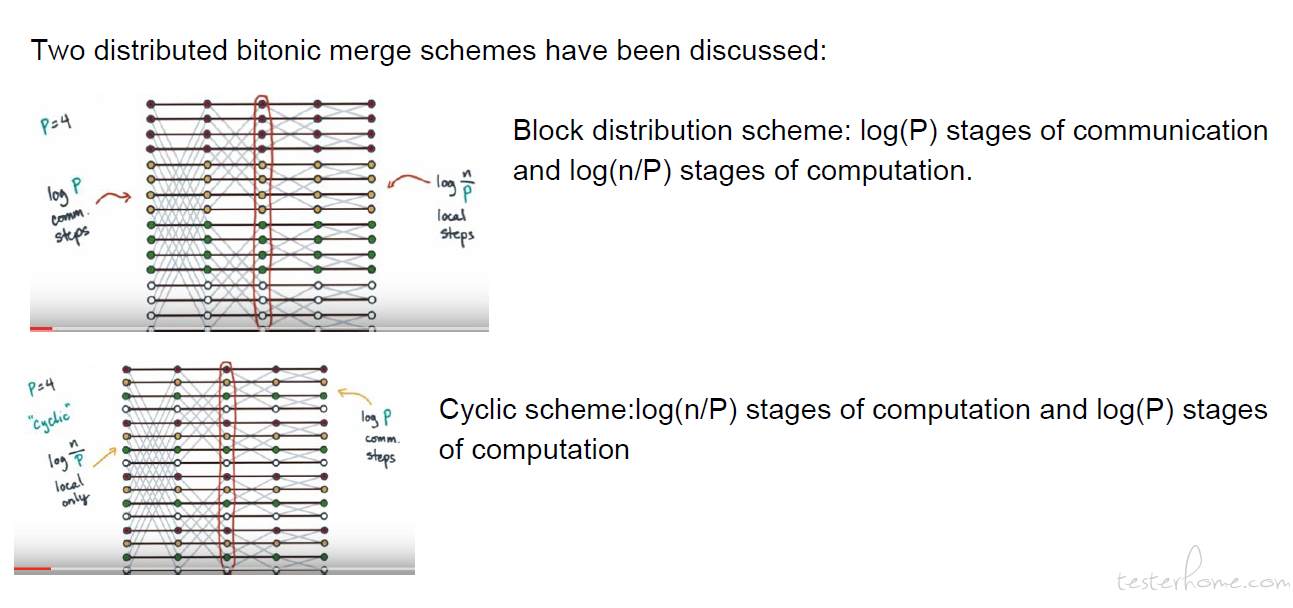
Bitonic Sort Cost Communication

计算时间

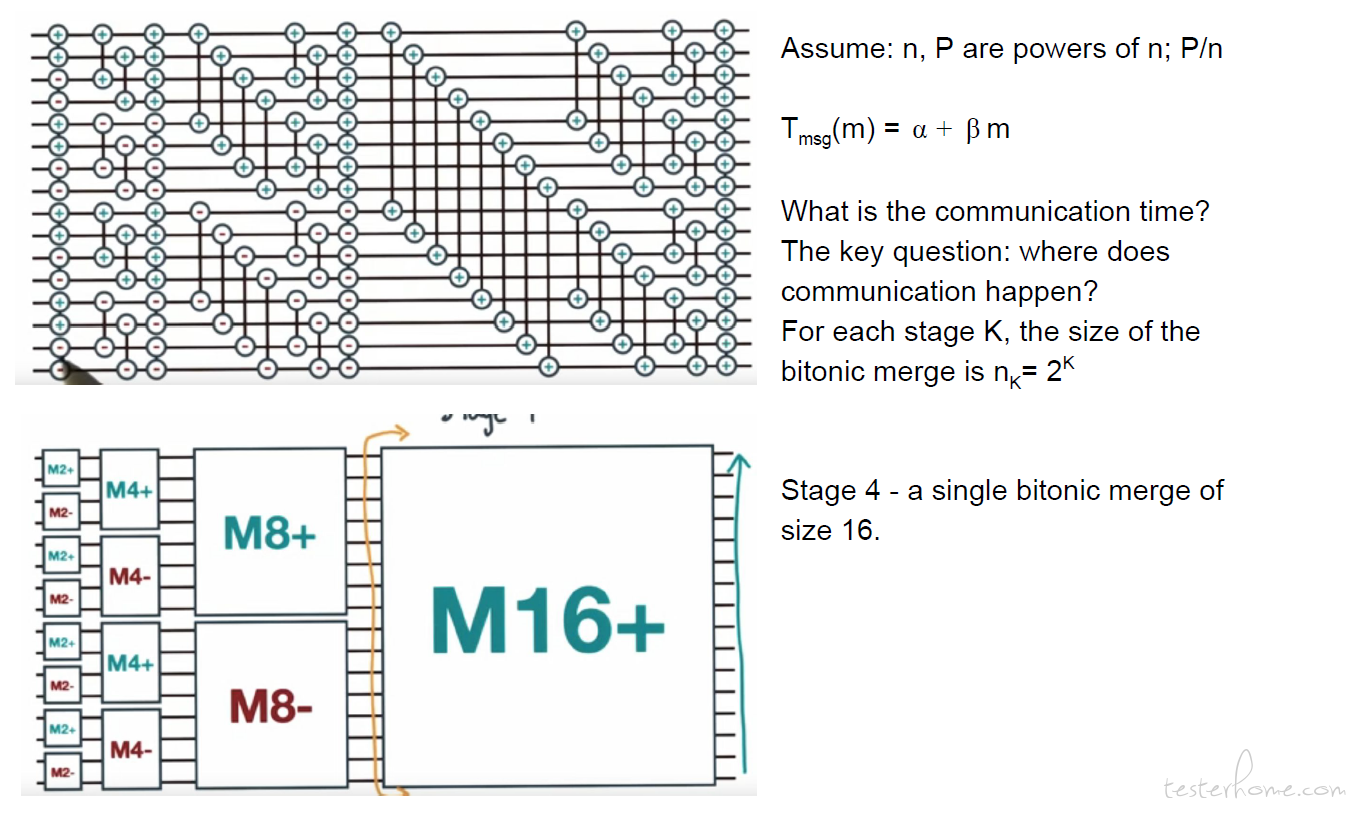
τ(n/P) K = total time to do the comparisons, at merging stage ‘K’
There are log n merging stages, so the total cost for computation is:

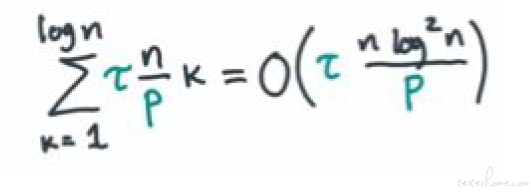
通讯时间

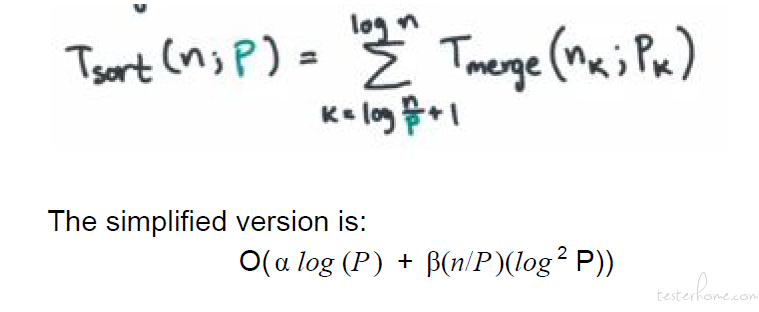
Linear Time Distributed Sort

桶排序

运行时间：

桶排序桶的采样：

大部分优秀的排序算法实际都是桶排序的变种？

Lesson 2.6 Distributed BFS

这一讲相当的水。。。
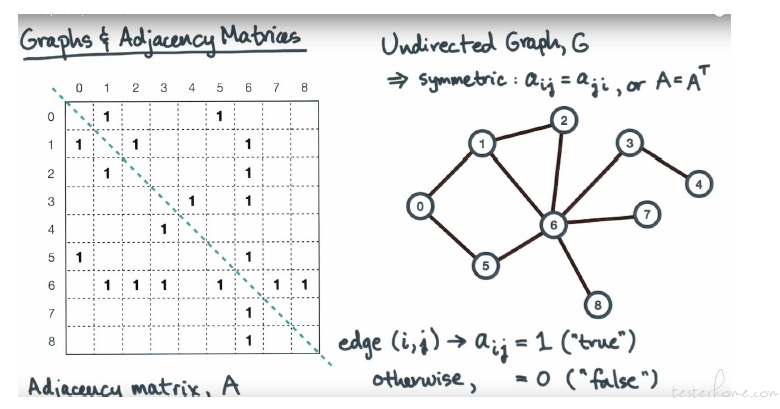
首先用一个 Adjacency Matrices 表示无向图。

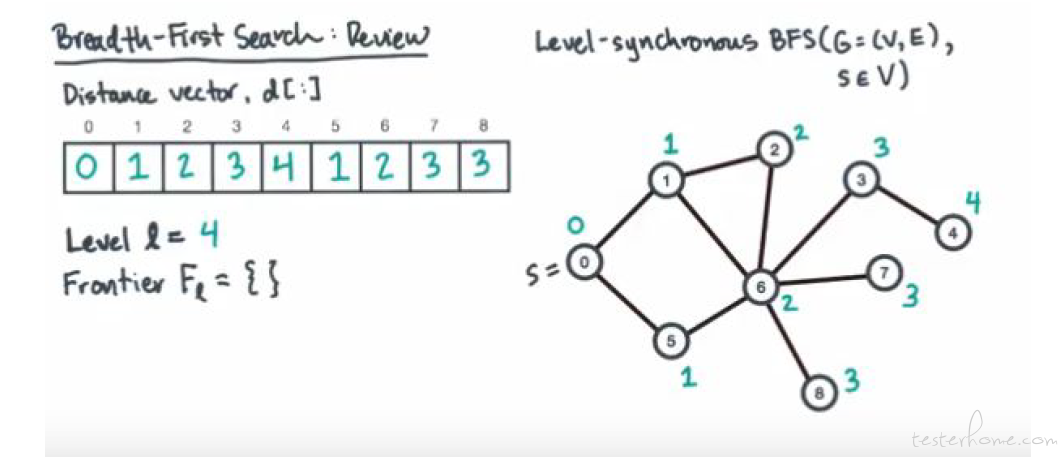
普通的 BFS 计算流程：

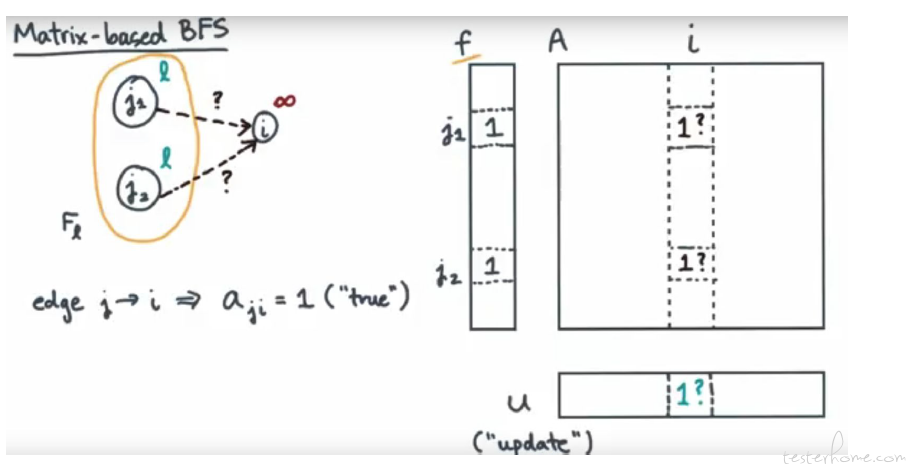
用 VECTOR 和矩阵乘法来计算需要更新的状态：

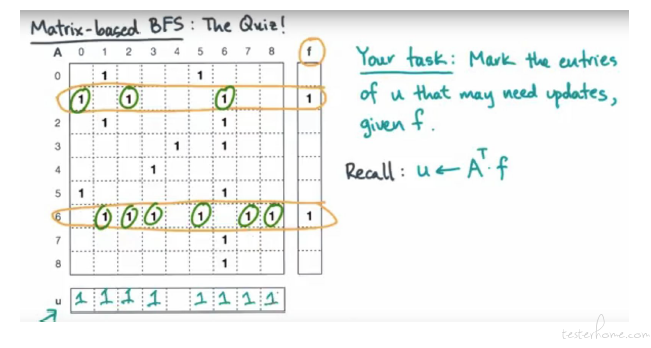
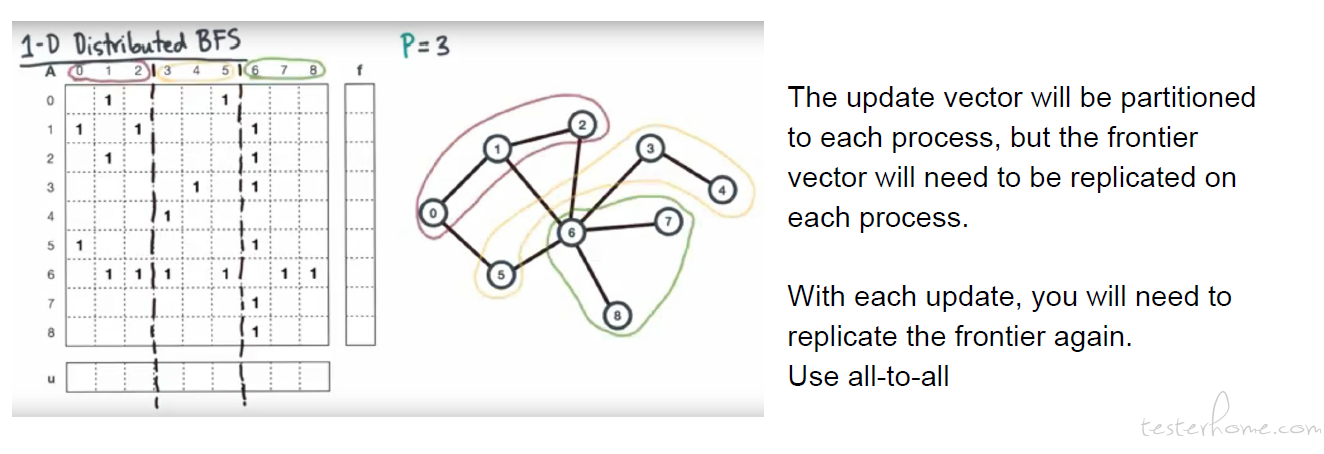
1D Distributed BFS

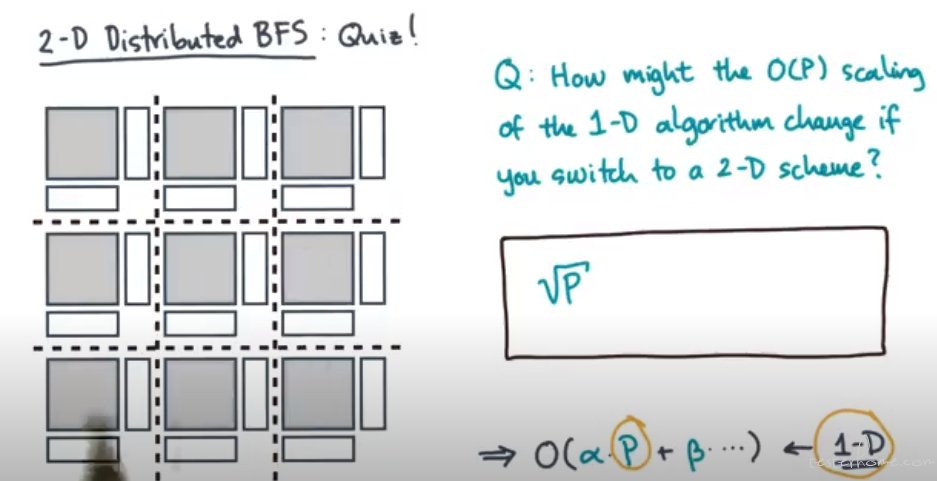
2D Distributed BFS

没说用什么方法来计算稀疏矩阵运算，一句话带过。感觉这才是核心。。。😓