padding
之前在讨论卷积神经网络的时候,我们是使用 filter 来做元素乘法运算来完成卷积运算的。目的是为了完成探测垂直边缘这种特征。但这样做会带来两个问题。
- 卷积运算后,输出图片尺寸缩小
- 越是边缘的像素点,对于输出的影响越小,因为卷积运算在移动的时候到边缘就结束了。中间的像素点有可能会参与多次计算,但是边缘像素点可能只参与一次。所以我们的结果可能会丢失边缘信息。
那么为了解决这个问题,我们引入 padding, 什么是 padding 呢,就是我们认为的扩充图片, 在图片外围补充一些像素点,把这些像素点初始化为 0. 如下图:
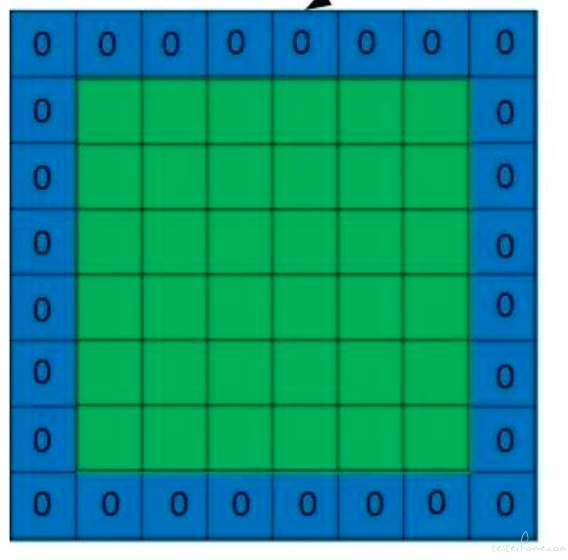
经过 padding 之后,原始图片尺寸为 (n+2p) x (n+2p),filter 尺寸为 f x f,则卷积后的图片尺寸为 (n+2p-f+1) x (n+2p-f+1)。若要保证卷积前后图片尺寸不变,则 p 应满足:
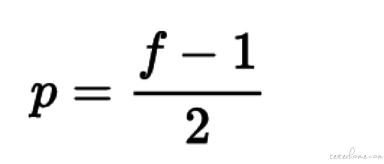
卷积步长 (Stride)
Stride 表示 filter 在原图片中水平方向和垂直方向每次的步进长度。若 stride=2,则表示 filter 每次步进长度为 2,即隔一点移动一次。
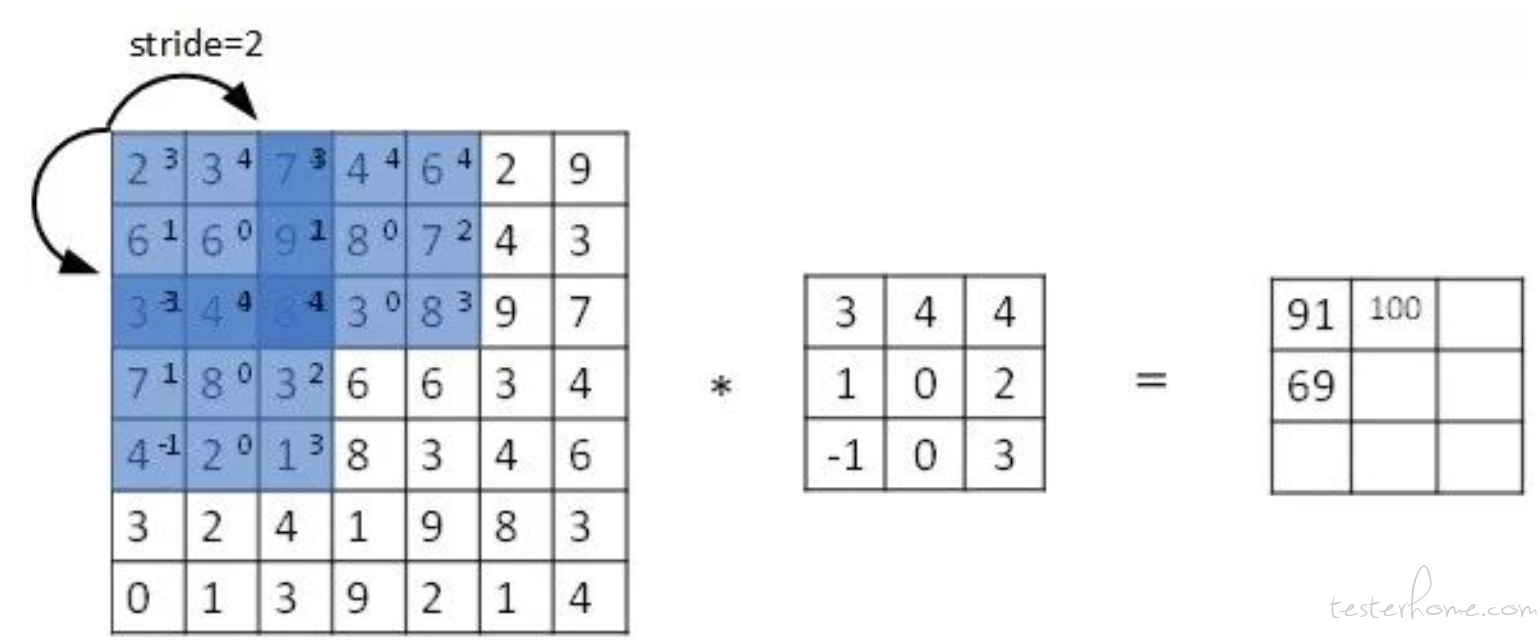
那么如果我们想要计算出任意一个卷积层输出图片的大小 (或者说维度的话),可以按照下面的公式计算。
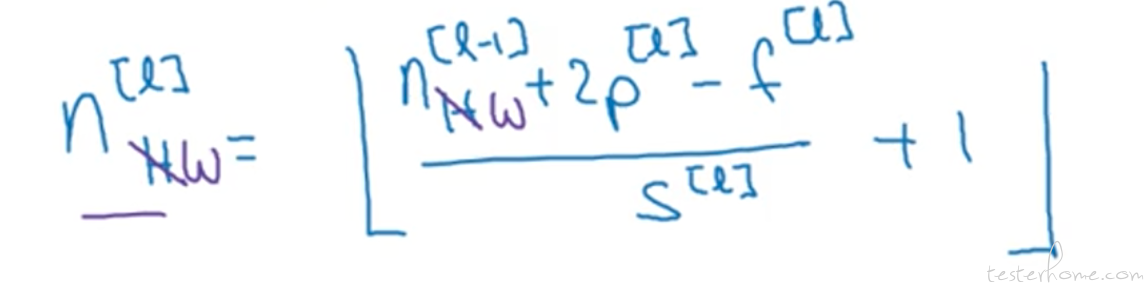
其中 n 为上一层图片的维度,p 是 padding, f 是过滤器的大小,s 是卷积步长。
单层神经网络
我们来总结一下,看上一节的一个卷积的图。
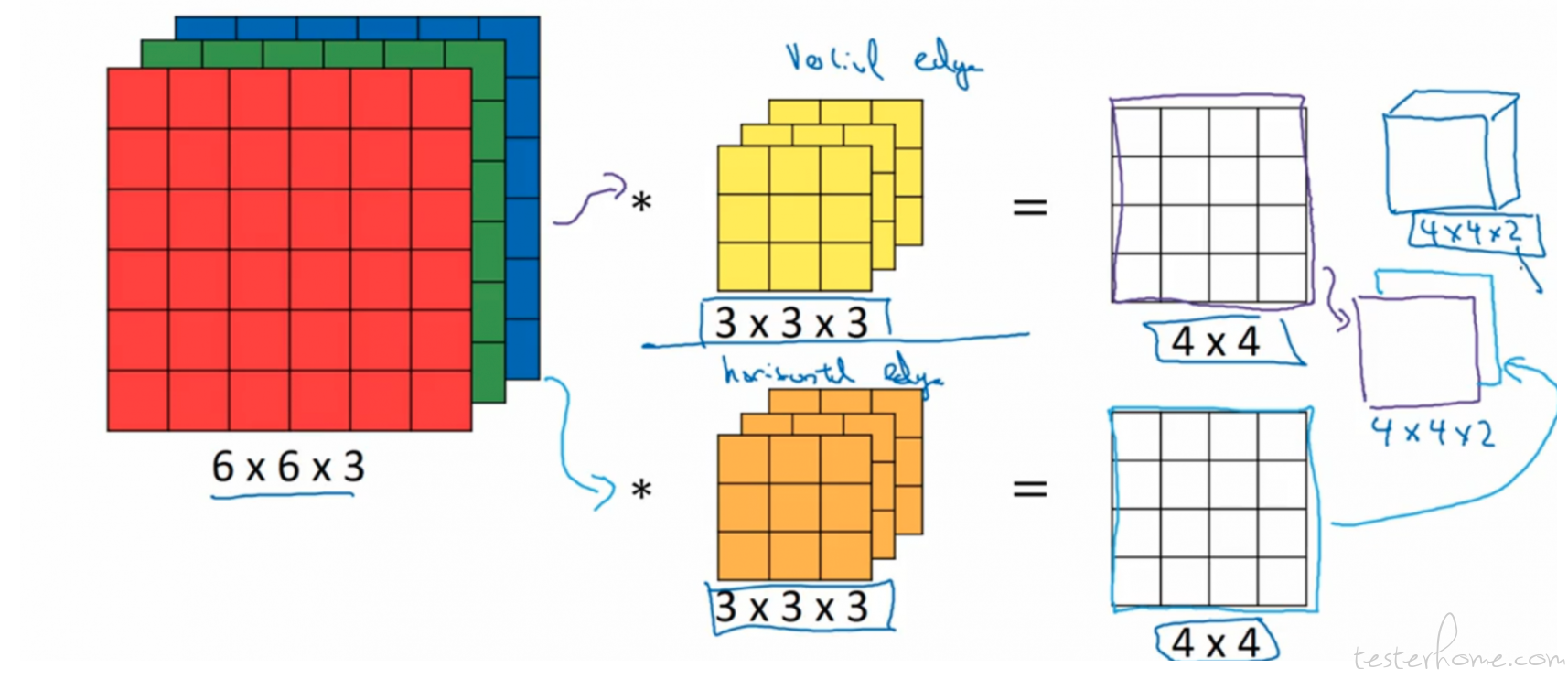
我们在神经网络中的每一层的计算公式都是 wx+b。 在卷积中也不例外。 那么在卷积中, 我们的过滤器中的参数就代表着 W,输入的图片的 RGB 矩阵就是 X(特征),同时我们再加入 b,就能完成一个神经元的计算了。
但是对于一个完整的卷积神经网络来说,除了卷积层,还有 pooling(池化层) 和 Fully connected(全连接层),我们先说 pooling
pooling
pooling 是用来减小尺寸,提高运算速度的,同时也可以减少噪声。它没有卷积计算,仅仅是在滤波器算子滑动区域内取最大值。如下:
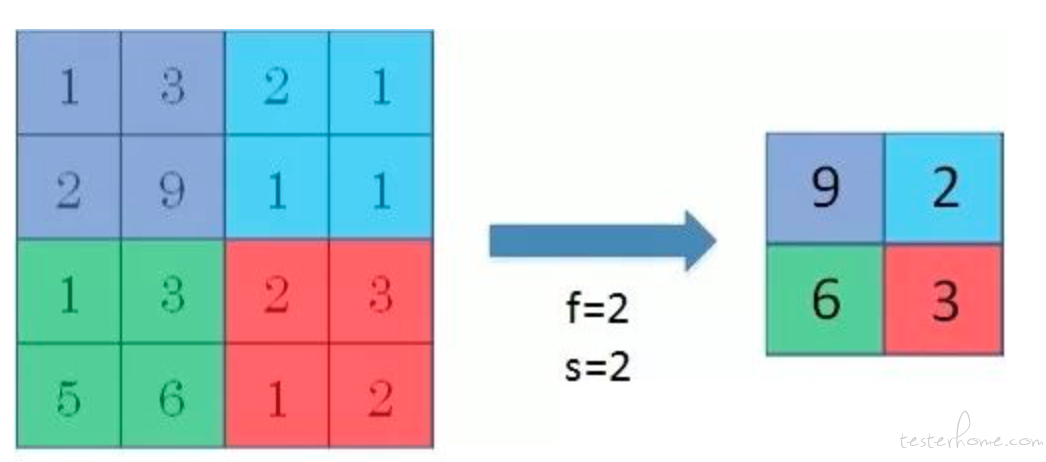
如上图, 我们在原始图片中做了卷积操作后,使用池化层来选取每一个区域中值最大的那个特征。 这就是池化层了。 它理解起来比较简单。
Fully connected
全连接层理解起来就更简单了。 它就是原本的神经网络里普普通通的一层。
一个完整的卷积神经网络的简单例子

如上图, 这个吴恩达深度学习课程中的一个卷积神经网络结构图。 一般来说我们都是在一个卷积层后跟着一个池化层,经历了多个这样的组合后。便开始使用全连接层。这样跟普通的神经网络一样,在最后的输出层中我们可以使用 sigmod 来做二分类或者 softmax 做多分类。