回顾

之前我们讲到了一些在训练模型的时候用到的超参数，例如上一次说的 L2 正则， 在过拟合的场景中增加 L2 的值有助于减小网络的复杂度。 还有诸如学习率， 在梯度下降中，每一次迭代的下降的步长是学习率乘以成本函数对 w 的导数。所以如果我们想让算法训练的快一点，调高学习率可以有效的减少迭代次数。 诸如此类的还有迭代次数，激活函数的选取等等。今天我们说一下 mini batch

什么是 mini batch

我们已知在梯度下降中需要对所有样本进行处理过后然后走一步，那么如果我们的样本规模的特别大的话效率就会比较低。假如有 500 万，甚至 5000 万个样本 (在我们的业务场景中，一般有几千万行，有些大数据有 10 亿行) 的话走一轮迭代就会非常的耗时。这个时候的梯度下降叫做 full batch。 所以为了提高效率，我们可以把样本分成等量的子集。 例如我们把 100 万样本分成 1000 份， 每份 1000 个样本， 这些子集就称为 mini batch。然后我们分别用一个 for 循环遍历这 1000 个子集。 针对每一个子集做一次梯度下降。 然后更新参数 w 和 b 的值。接着到下一个子集中继续进行梯度下降。 这样在遍历完所有的 mini batch 之后我们相当于在梯度下降中做了 1000 次迭代。 我们将遍历一次所有样本的行为叫做一个 epoch，也就是一个世代。 在 mini batch 下的梯度下降中做的事情其实跟 full batch 一样，只不过我们训练的数据不再是所有的样本，而是一个个的子集。 这样在 mini batch 我们在一个 epoch 中就能进行 1000 次的梯度下降，而在 full batch 中只有一次。 这样就大大的提高了我们算法的运行速度。

mini batch 的效果

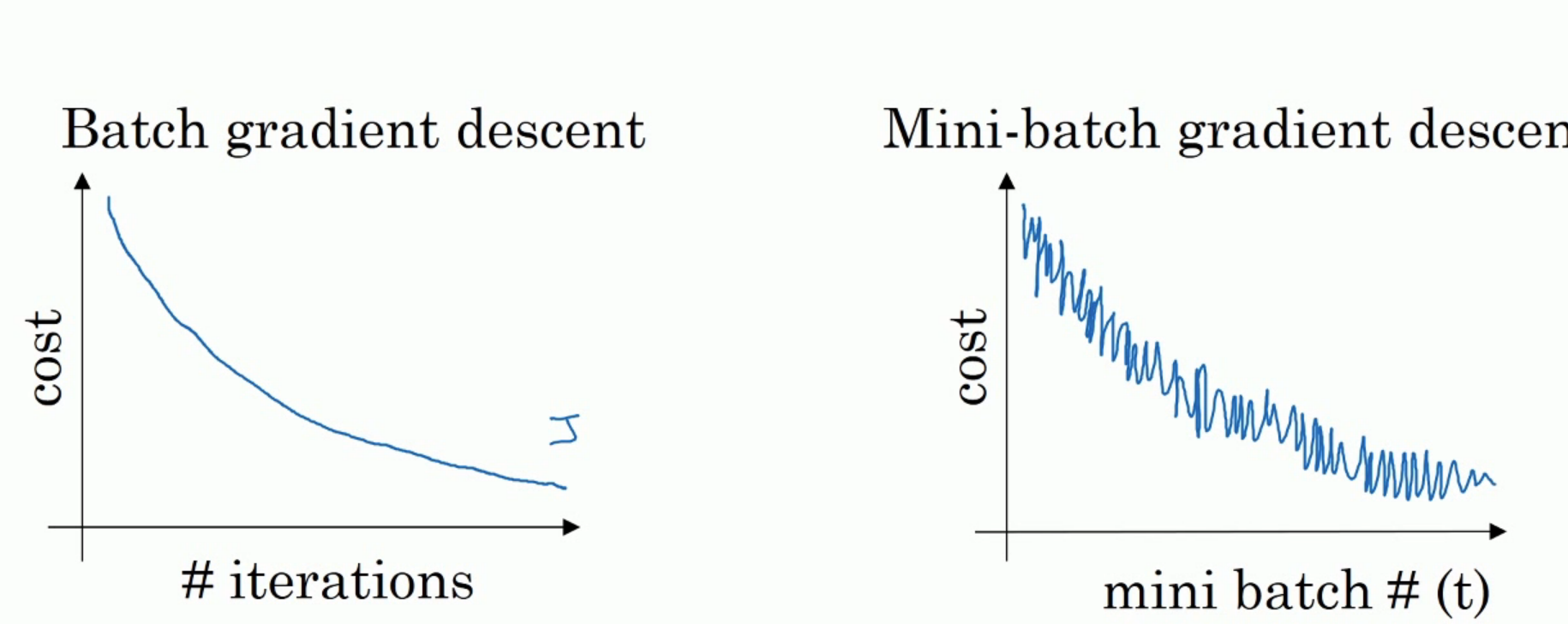
如上图，左边是 full batch 的梯度下降效果。 可以看到每一次迭代成本函数都呈现下降趋势，这是好的现象，说明我们 w 和 b 的设定一直再减少误差。 这样一直迭代下去我们就可以找到最优解。 右边是 mini batch 的梯度下降效果，可以看到它是上下波动的，成本函数的值有时高有时低，但总体还是呈现下降的趋势。 这个也是正常的，因为我们每一次梯度下降都是在 min batch 上跑的而不是在整个数据集上。 数据的差异可能会导致这样的效果 (可能某段数据效果特别好，某段数据效果不好)。但没关系，因为他整体的是呈下降趋势的。

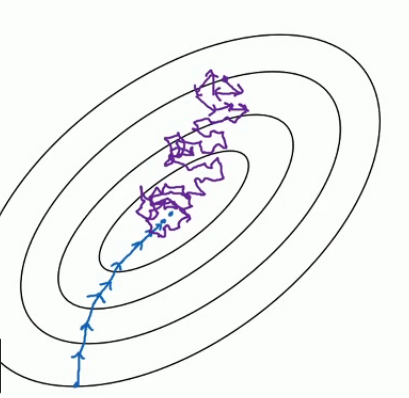
把上面的图看做是梯度下降空间。 下面的蓝色的部分是 full batch 的而上面是 mini batch。 就像上面说的 mini batch 不是每次迭代损失函数都会减少，所以看上去好像走了很多弯路。 不过整体还是朝着最优解迭代的。 而且由于 mini batch 一个 epoch 就走了 5000 步，而 full batch 一个 epoch 只有一步。所以虽然 mini batch 走了弯路但还是会快很多。

经验公式

既然有了 mini batch 那就会有一个 batch size 的超参数，也就是块大小。代表着每一个 mini batch 中有多少个样本。 我们一般设置为 2 的 n 次方。 例如 64,128,512,1024. 一般不会超过这个范围。不能太大，因为太大了会无限接近 full batch 的行为，速度会慢。 也不能太小，太小了以后可能算法永远不会收敛。 当然如果我们的数据比较小， 但也用不着 mini batch 了。 full batch 的效果是最好的。

结尾

这周没时间了先更这点，赶紧睡觉明天赶火车了