Parser

简介

前面介绍的词法分析，并不能分析语言的结构。比如 if 嵌套。
那么就需要引入 Parser 来进行分析。

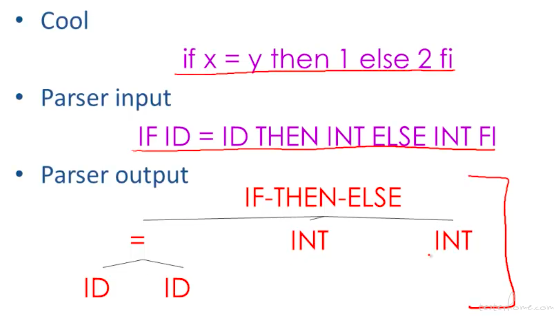
Context free grammar（上下文无关文法）

程序语言都会有递归的结构，比如表达式其实就是一种递归。

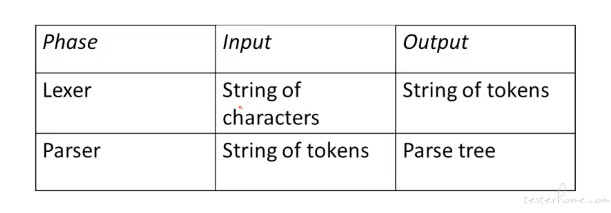
组成部分

解析

转化 production 的例子：

CFG 的定义：

一个 EXPR 的例子：

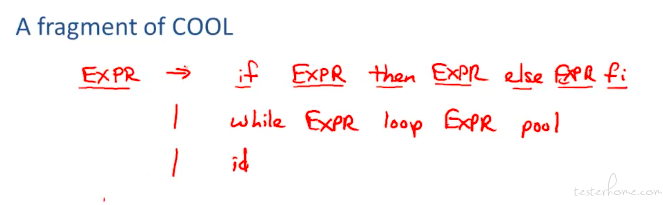
可以看到在很多种情况下，内容都可以翻译成 EXPR。
一个算术表达式的例子：

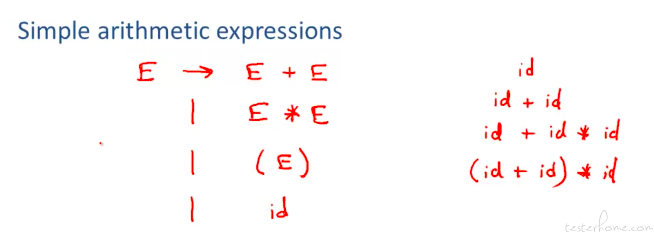
上下文无关文法概念总结：

Derivations

定义

举例：

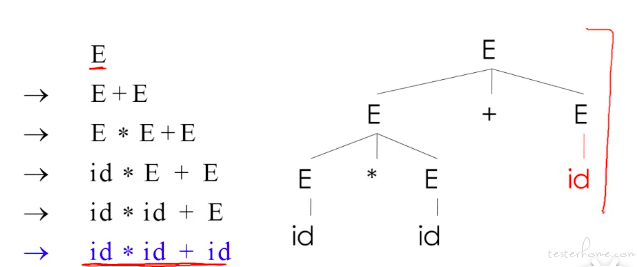
parse tree 属性：

最左最右推导可以看这篇文章：
https://blog.csdn.net/weixin_44226857/article/details/104240028

ambiguity

对于相同的 EXPR，使用不同的推导方式会得到可能不同的结果。


可以通过重新修改语法来避免歧义。
如上文，+ 和使用不同的语义，修改后的优先级会高于 +。可以关注一下 () 的定义，可以看到（）内转化的都是 E 而不是 E'。

继续以 if-then-else 举例说明歧义：

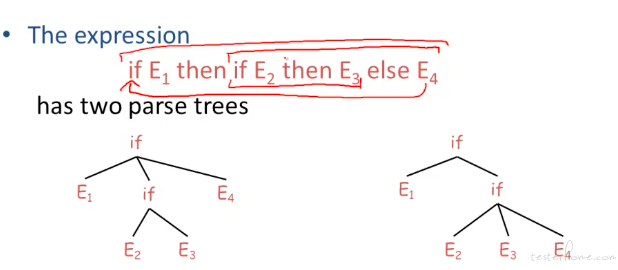
通过定义如下的语义解决：

重写语法的成本相对较高，也可以通过其他方式来解决歧义。

precedence and associativity

异常处理

异常处理需要实现的内容：

panic mode

举例：

Error productions

这个就要改语法了。

Error correction

异常处理的现状

抽象语法树（AST）

定义：

举例说明：5+（2+3）


对于 parser tree 来说，有部分信息是没有价值的，比如 E-int,可以直接用 int 替换。（E）从树的结构中就可以看到有（）操作符

抽象语法树结构：

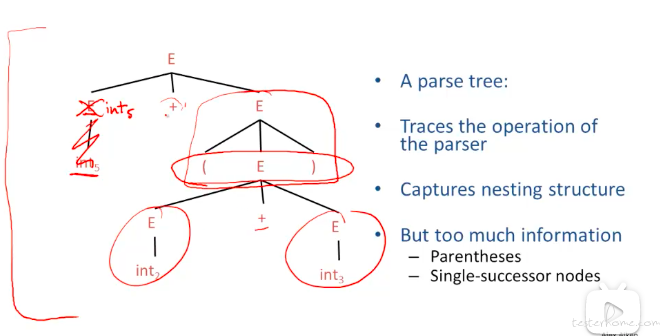
Recursive decent parsing(递归下降语法)

举例说明：

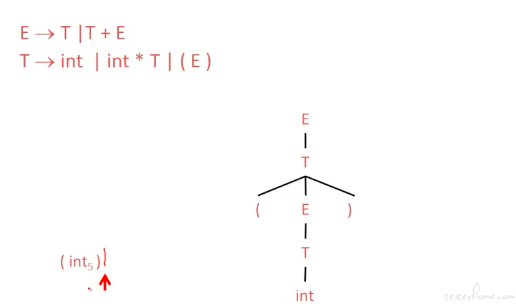
RDA（Recursive decent algorithm）

这个方法，下面会讲它有问题的地方。

RDA（Recursive decent algorithm）的缺陷

在本例中，int*int,第一个 int 被解析程 T，直接返回。整个输入应该没有被消耗结束。

通常的递归下降算法应该支持全部的递归。

Left Recursion

左递归会导致无限循环。
可以通过修改语法来解决问题：

更通常的解法：

两步可能出现的问题：

这里对应龙书算法 4.19，具体就不深究了。

递归下降总结：

重点
需要理解什么是正则文法，什么是上下文无关文法，什么时候会造成歧义，RDA 的概念和简单实现，如何翻译左回归的问题
做题的时候发现，有限长度的表达式都可以转化成正则。
无限长度的的 1 个特例：0ⁿ 1ⁿ
这是一个上下文无关非正则的文法。
S->0S1 | E