前言

相信大家之前都了解过很多种树据结构，我之前总是两两的，也就是从局部上去进行比较，没有从整体上进行这些树的发展脉络进行梳理，因此经常看完没多久就忘了。看来确实是需要从本源出发，不仅要知其然还要知其所以然，了解清楚前因后果，不仅可以方便我们记忆，更有利于增加我们的理解深度。实际上任何事物的出现都是有他出现的必要性，当某个事物达到瓶颈之后，必然会出现新的事务来弥补它的不足。好的，废话不多说了，今天我们就从一个小的 BST 开始，一起见证一下它的升级打怪之路吧。

开场之前，先来两颗开胃小树

完全二叉树：

金无足赤，人无完人，但是二叉树是可以有完美的，所有叶子都位于相同的水平的二叉树就是完全二叉树。

平衡二叉树：

树也是有等级之分的，不是所有的树都是完美的，相比完美二叉树，稍微低一等级的叫平衡二叉树。每个节点的平衡因子在-1到1之间的，虽然不是完全平衡的，但是也还能接受。

二叉搜索树 (BST)：

二叉搜索树（balance search tree），这是一棵有组织有纪律的树，满足左子树中所有节点的值小于根的值，右子树中所有节点的值大于或等于根的值。简单说就是有序的，所以在查询的时候就可以使用二分法，因此具有很高的查询效率，最佳的时间复杂度是 o(log n)，最差是O(n)。当一颗二叉搜索树是一组升序或者降序的数值时，二叉搜索树就会退化为单链表，查找时间复杂度变成了O(n)。

AVL 树

为什么会有 AVL 树

前边提到了，当向 BST 中插入一组有序的数值时，就会退化为单链表，性能会退化到 o(n)，究其根源是因为小时候父母管的比较松，任由她自由发展，导致 BST 偏科了，能力没有得到均衡发展，所以怎么办呢？嗯，没错，是得请个家教，而且一个不够，得两个，制定个规则去约束她，即使不能像完美二叉树那样科科满分，至少也得平衡一些是吧，要不都嫁不出去啦。请了家教之后，BST 直接鸟枪换炮，摇身一变成为了我们接下来要介绍的 AVL 树。

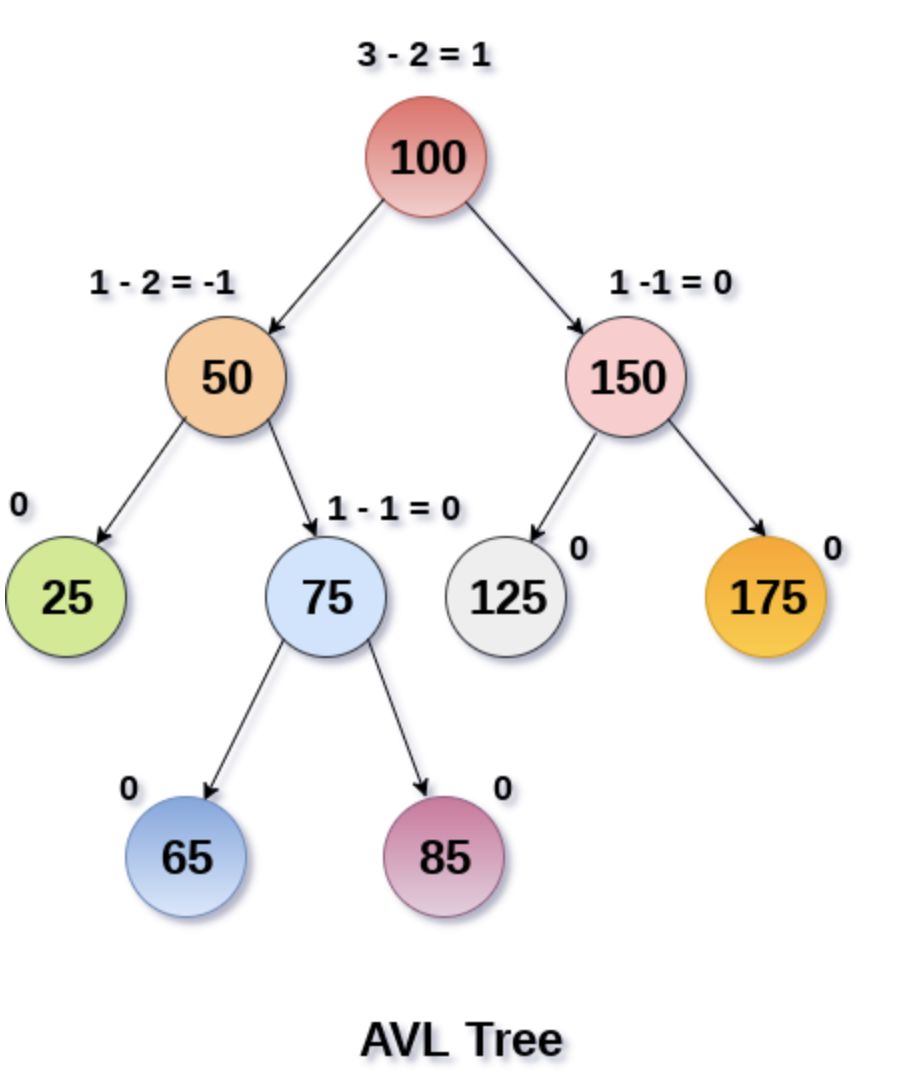
什么是 AVL 树

AVL 树指的是平衡二叉搜索树，没错它就是二叉搜索树和平衡二叉树杂交育种的结果，结合了双亲的优良特性，有序且平衡，直接走向树生巅峰。

为什么叫 AVL 树？这可不是取的平衡二叉搜索树首字母的缩写，而是因为是 BST 的两个家教的 name 是G. M. Adelson-Velsky和Evgenii Landis。

AVL 树的查找，插入和删除的时间复杂度都固定是 o(log n)，但是增加和删除操作会使树失去平衡，因此需要通过一次或多次树旋转来重新平衡这棵树。

旋转分为 LL，LR，RR，RL4 种方式，具体的插入和删除的情况比较多，在这就不详细展开了，说一下关键的一点，是可能需要多次旋转来维持平衡，因此维护树保持平衡的成本还是蛮高的嘞，这也正是 AVL 树的弊端。

红黑树

为什么会出现红黑树

AVL 树的左右子树高度差不能超过 1，每次进行插入/删除操作时，几乎都需要通过旋转操作保持平衡，在频繁进行插入/删除的场景中，频繁的旋转操作使得 AVL 的性能大打折扣，所以就有了红黑树的出现。

什么是红黑树

红黑树是一种自平衡的二叉搜索树，和 AVL 树十分类似，红黑树的查找，插入和删除的时间复杂度都是 o(log n)。但是红黑树不是一颗严格的平衡二叉树，它不像 AVL 树那样严格维持平衡因子为 1 来保持平衡，而是通过左旋，右旋和变色3 种操作，维持自身的 5 大特性，保证了最长路径不超过最短路径的两倍，从而实现近似的平衡。

红黑树和 AVL 树的对比：

查找，插入和删除的时间复杂度都是 o(log n)，相比于 AVL 树，红黑树牺牲了部分的平衡性，来换取了在插入和删除时更少的旋转的操作，因为整体性能上要优于 AVL 树，所以在查询场景多，插入和删除稍作少的场景，AVL 树的性能更好，当插入和删除场景很多的时候，红黑树的性能更佳。

B 树

为什么会出现 B 树

传统用来搜索的平衡二叉树有很多，如 AVL 树，红黑树等。这些树在一般情况下查询性能非常好，但当数据非常大的时候它们就无能为力了。原因当数据量非常大时，内存不够用，大部分数据只能存放在磁盘上，只有需要的数据才加载到内存中。一般而言内存访问的时间约为 50 ns，而磁盘在 10 ms 左右。速度相差了近 5 个数量级，磁盘读取时间远远超过了数据在内存中比较的时间。这说明程序大部分时间会阻塞在磁盘 IO 上。那么我们如何提高程序性能？减少磁盘 IO 次数，像 AVL 树，红黑树这类平衡二叉树从设计上无法 “迎合” 磁盘。

平衡二叉树是通过旋转来保持平衡的，而旋转是对整棵树的操作，若部分加载到内存中则无法完成旋转操作。其次平衡二叉树的高度相对较大为 log n（底数为 2），这样逻辑上很近的节点实际可能非常远，无法很好的利用磁盘预读（局部性原理），所以这类平衡二叉树在数据库和文件系统上的选择就被 pass 了。

什么是 B 树

B 树是一种多路平衡查找树，相对于二叉树而言，B 树可以认为是一颗多叉树，m 阶 B 树表示一个节点最多有 m 个子节点。

下面我们来看看 B 树的定义。

• 每个节点最多有 m-1 个关键字（可以存有的键值对）。
• 根节点最少可以只有 1 个关键字。
• 非根节点至少有 m/2 个关键字。
• 每个节点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
• 所有叶子节点都位于同一层，或者说根节点到每个叶子节点的长度都相同。
• 每个节点都存有索引和数据，也就是对应的 key 和 value。

所以，根节点的关键字数量范围：1 <= k <= m-1，非根节点的关键字数量范围：m/2 <= k <= m-1。

B 树和 AVL 树、红黑树一样，也是一颗自平衡的查找树，当新插入的节点不满足要求时，也会进行维权运动，只不过 B 树不会去旋转了，而是分裂，核心临界条件是每个节点关键字的数量，如果数量超出要求，那她就会进行分裂。

简单说一下分裂的过程，假如一颗 4 阶 B 树，当新插入元素后，某个节点的关键字数量达到 4 个，因为每个节点最多有 m-1 个关键字，也就是最多只能有 3 个节点，这时候就需要进行分裂。假设 key 的值为 5，6，7，8，那会以 m/2 为界分为 3 个部分，5---6---7，8，分裂会将 6 放入父节点，5 和 7，8 两个节点分别指向父节点。

这也就是说 B 树的分裂只会影响父节点和当前节点。

B+ 树

什么是 B+ 树

特性：

1. B+ 树包含 2 种类型的节点：内部节点（也称索引节点）和叶子节点。根节点本身即可以是内部节点，也可以是叶子节点。根节点的关键字 key 个数最少可以只有 1 个；
2. B+ 树与 B 树最大的不同是内部节点不保存数据，只用于索引，所有数据（或者说记录）都保存在叶子节点中；
3. m 阶 B+ 树表示了内部节点最多有 m-1 个关键字（或者说内部节点最多有 m 个子树，和 B 树相同），阶数 m 同时限制了叶子节点最多存储 m-1 个记录；
4. 内部节点中的 key 都按照从小到大的顺序排列，对于内部节点中的一个 key，左树中的所有 key 都小于它，右子树中的 key 都大于等于它。叶子节点中的记录也按照 key 的大小排列；
5. 每个叶子节点都存有相邻叶子节点的指针，叶子节点本身依关键字的大小自小而大顺序链接；

B+ 树和 B 树的对比：

B+ 树和 B 树的核心区别是，B 树的每个节点都存储索引和数据，而 B+ 树只有叶子节点存储了索引和数据，非叶子节点只存储索引，B+ 树相对于 B 树的优点，有如下 3 点：

• 磁盘 IO 次数少

因为 B+ 树只有叶子节点存储了数据，其他非叶子节点只保存和索引，所以 B+ 树单次磁盘 IO 的数量是要大于 B 树的，这就意味着 B+ 树可以减少磁盘 IO 的次数，而我们都知道访问磁盘的速度比直接访问内存，要慢了不知道多少倍，所以磁盘 IO 的次数往往会成为性能的瓶颈点，因此磁盘 IO 次数少，可以大幅的提升插入和查询效率。

• 适合范围查询

B+ 树叶子节点形成有序链表，范围查询转化为顺序读，效率高。相对而言 B 树必须通过中序遍历才能支持范围查询。

• 查询性能稳定

因为 B+ 树的数据全都保存在叶子节点上，因此每次必须要遍历到叶子节点，因此查询时间复杂度固定为 O(log n)，而 B 树的数据直接保存在每个节点上，因此 B 树的查询时间复杂度在 O(1) 和 O(log n) 之间。

B+ 树的缺点

B+ 树的主要缺点有两个：

• 如果写入的数据比较离散，那么寻找写入位置时，子节点有很大可能性不会在内存中，最终会产生大量的随机写，性能下降。
• 如果 B+ 树已经运行了很长时间，写入了很多数据，随着叶子节点分裂，其对应的块会不再顺序存储，而变得分散。这时执行范围查询也会变成随机读，效率降低了。

LSM 树

为什么会出现 LSM 树

B+ 树作为 mysql 的索引结构，长期以来主流使用 B+ 树这种索引结构来实现快速数据查找，具有很好的读性能。当数据量不太大时，B+ 树读写性能表现也非常好。但是在海量数据情况下，经常性的会有大量的数据的写入和更新，B+ 树越来越高，由于 B+ 树更新和删除数据时需要沿着 B+ 树逐层进行页分裂和页合并，当有大量分裂时，会导致大量的磁盘随机寻道，严重影响数据写入性能。LSM-tree 就是为了解决上述问题而生的一种存储结构。

什么是 LSM 树

LSM Tree 出现于谷歌的三驾马车之一的《Bigtable: A Distributed Storage System for Structured Data》，全称为 Log-Structured Merge Tree，是一个分层、有序、针对块存储设备（机械硬盘和 SSD）特点而设计的数据存储结构。

很多流行的数据库都有它的身影，比如 Cassandra、RocksDB、HBase、LevelDB 等 NoSQL 数据库，TiDB 等 newSQL 数据库，甚至像 SQLite 这种传统的关系型数据库和 MongoDB 这种传统的文档型数据库，以及 clickhouse 都提供了基于 LSM Tree 的存储引擎作为可选的存储引擎。

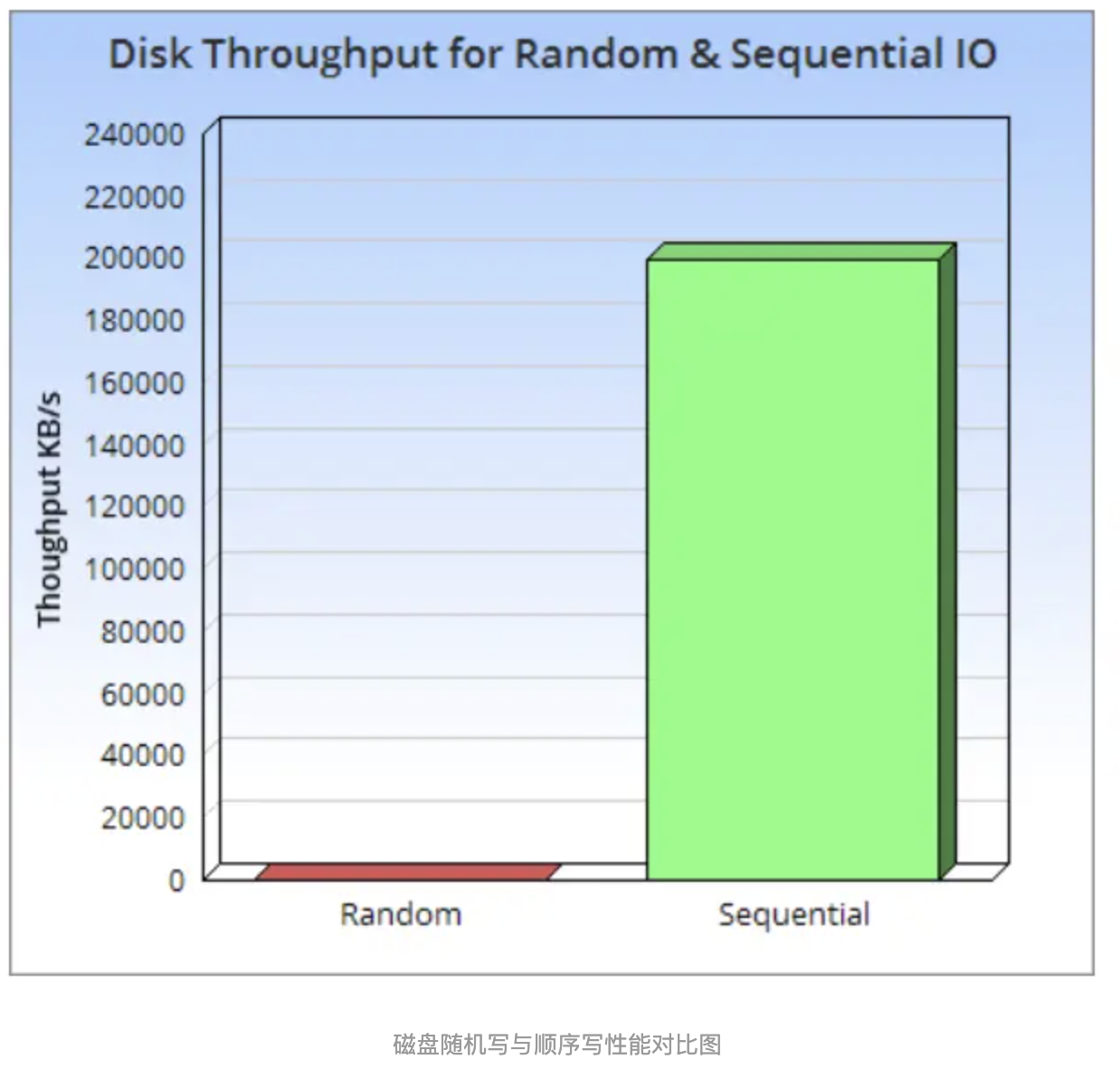
它的核心理论基础还是磁盘的顺序写速度比随机写速度快非常多，即使是 SSD，由于块擦除和垃圾回收的影响，顺序写速度还是比随机写速度快很多。

基本组成

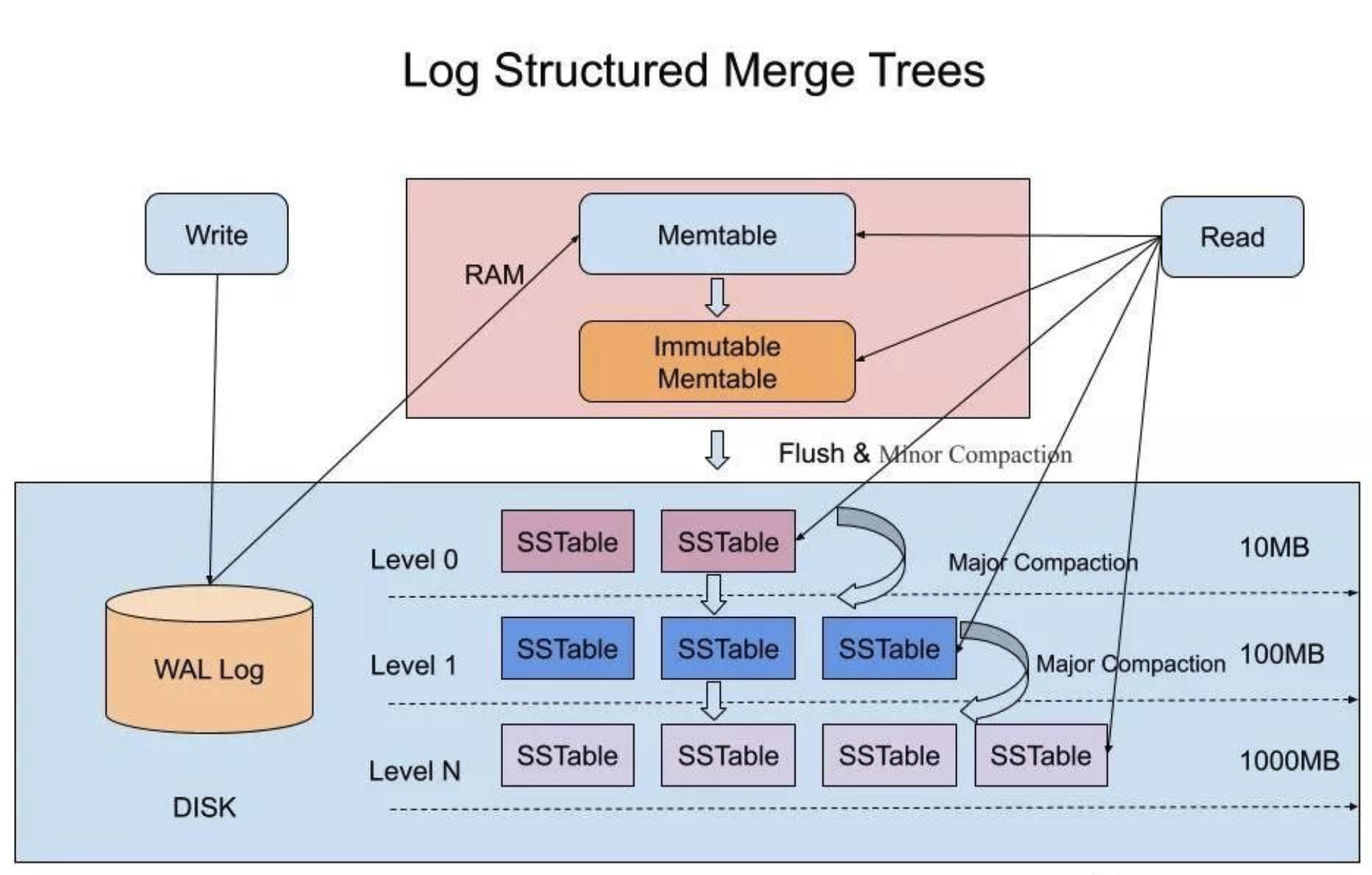
• WAL（write ahead log）

WAL 的结构和作用跟其他数据库一样，是一个只能在尾部以 Append Only 方式追加记录的日志结构文件，它用来当系统崩溃重启时重放操作，使 MemTable 和 Immutable MemTable 中未持久化到磁盘中的数据不会丢失。

• MemTable

MemTable 是内存中的数据结构，用于写入和读取最近更新的数据，MemTable 具体的数据结构，LSM 并没有强约束，可以是红黑树，也可以是跳表结构。需要支持高效的动态插入数据，对数据进行排序，也支持高效的对数据进行精确查找和范围查找。

• Immutable MemTable

当 MemTable 达到阈值的大小后，会转化为 Immutable MemTable。Immutable MemTable 不能写数据，只能读数据，定期会将 Immutable MemTable 的数据 flush 到磁盘中。

• SSTable(Sorted String Table)

SSTable 是一种拥有持久化，有序且不可变的的键值存储结构，它的 key 和 value 都是任意的字节数组，并且了提供了按指定 key 查找和指定范围的 key 区间迭代遍历的功能。SSTable 内部包含了一系列可配置大小的 Block 块，典型的大小是 64KB，关于这些 Block 块的 index 存储在 SSTable 的尾部，用于帮助快速查找特定的 Block。当一个 SSTable 被打开的时候，index 会被加载到内存，然后根据 key 在内存 index 里面进行一个二分查找，查到该 key 对应的磁盘的 offset 之后，然后去磁盘把响应的块数据读取出来。当然如果内存足够大的话，可以直接把 SSTable 直接通过 MMap 的技术映射到内存中，从而提供更快的查找。

写流程

LSM-tree 写入数据时，会先写一条记录到 WAL 中，然后会将数据写入内存中的 MemTable 中，当然内存的大小肯定是有限制的，不可能一直往里写，当 MemTable 的大小达到设定的阈值后，MemTable 会转换为 Immutable MemTable，顾名思义就是不可变的 MemTable，然后会生成一个新的 MemTable，用来写入新的数据。所以说 MemTable 只会有一个，但是 Immutable MemTable 可能会有多个。会有单独的线程定期的将 Immutable MemTable 的数据 flush 到磁盘中的 SSTable 中。

删数数据的时候与写入新数据一样，都是写入一条新的记录，只是删除数据时会添加一个删除标记，只有再 compact 时才会对带有删除标记的数据进行物理删除。

读流程

先在内存MemTable中查找，然后在内存中的Immutable MemTable中查找，然后在level 0 SSTable中查找，最后在level N SSTable中查找。

查找某个具体的 SSTable 时，一般先把 SSTable 的元数据 block 读到内存中，根据BloomFilter可以快速确定数据在当前 SSTable 中是否存在，如果存在，则采用二分法确定数据在哪个数据 block，然后将相应数据 block 读到内存中进行精确查找。

从LSM Tree数据查找过程我们可以看到，为了查找到目标数据，我们需要读取并查找不包含目标数据的 SSTable，如果目标数据在最底层 level N 的 SSTable 中，我们需要读取和查找所有的 SSTable！LSM Tree把这种读取和查找了无关 SSTable 的现象叫做读放大 (read amplification)。

读放大现象严重影响了LSM Tree数据查找性能，论文《BigTable》提到了几种提升数据查找性能的方法，如压缩，缓存，索引 (布隆过滤器) 以及compact等操作，这里就不详细展开了。

LSM 树和 B+ 树的对比

LSM 树和 B+ 树的差异主要在于读性能和写性能进行权衡

当写多读少的场景，LSM 树相比于 B 树有更好的性能。因为大量的插入操作，为了维护 B+ 树结构，节点分裂。读磁盘的随机读写概率会变大，性能会逐渐减弱。

当读多写少的场景，B+ 树相比于 LSM 树有更好的性能。LSM 树通过牺牲部分读性能为代价，来大幅提升写性能，并且通过一些优化手段，如布隆过滤器和 compact 策略，对读性能有了很大的优化，时间复杂度也是 O(log n) 级别的。

参考文档：

https://www.cnblogs.com/wxiaotong/p/14781753.html

https://www.jianshu.com/p/f911cb9e42de

作者：京东物流 于建飞

来源：京东云开发者社区 自圆其说 Tech 转载请注明来源