新手区一些常见的字符串匹配算法

京东云开发者 · 2023年04月25日 · 678 次阅读

作者：京东零售李文涛

一、简介

1.1 Background

字符串匹配在文本处理的广泛领域中是一个非常重要的主题。字符串匹配包括在文本中找到一个，或者更一般地说，所有字符串 (通常来讲称其为模式) 的出现。该模式表示为 p=p[0..m-1];它的长度等于 m。文本表示为 t=t[0..n-1],它的长度等于 n。两个字符串都建立在一个有限的字符集上。

一个比较常见的字符串匹配方法工作原理如下。在一个大小通常等于 m 的窗口帮助下扫描文本。首先将窗口和文本的左端对齐，然后将窗口的字符与文本中的字符进行比较，这一特定的工作被称为尝试，在完全匹配或不匹配之后，将窗口移到右侧。继续重复同样的过程，直到窗口的右端超过文本的右端，一般称为滑动窗口机制。

1.2 Brute force

BF 算法检查文本中 0 到 n-m 之间的所有位置，是否有模式从那里开始出现。然后，在每次尝试之后，它将模式串向右移动一个位置。

BF 算法不需要预处理阶段，除了模式和文本之外，还需要一个恒定的额外空间。在搜索阶段，文本字符比较可以以任何顺序进行。该搜索阶段的时间复杂度为 O(mn)。

public static int strMatch(String s, String p){
    int i = 0, j = 0;
    while(i < s.length() && j < p.length()){
        if(s.charAt(i) == p.charAt(j)){
            i++;
            j++;
        }else{
            i = i - j + 1;
            j = 0;
        }
        if (j == p.length()){
            return i - j;
        }
    }
    return -1;
}

二、KMP

先回顾下 brute force 中匹配的情况。我们在文本串 BBC#ABCDAB$ABCDABCDABDE 中查找模式串 ABCDABD，文本串中第 1 个字符 “B” 与模式串中第 1 个字符 “A” 不匹配，所以我们将模式传后移一位。

文本串中的第 2 个字符 “B” 和模式串中的第一个字符 “A” 不匹配，继续后移。

基于这种方式不断比较并且移动，我们发现文本串中的第 5 个字符 “A” 和模式串中的第 1 个字符 “A” 是匹配的，那么继续比较文本串和模式串的下一个字符。

不断比较之后我们发现，文本串中的字符 “$” 和模式串中的最后一个字符 “D” 不匹配。

根据 BF 算法，我们应该继续将模式串向后移动一位，然后从头开始重新比较。

那我们不妨观察下，上次匹配失败的情况，当文本串中 “$” 与模式串中 “D” 不匹配时，我们其实已经完成了 6 次匹配，也就是说我们在文本串和模式串中已经找到了"ABCDAB"。同时我们可以发现模式串中前缀 “AB” 是可以和文本串中已匹配成功部分的后缀 “AB” 相匹配，我们利用这个信息，可以把模式串右移多位，而不仅仅是 1 位来去继续匹配（换句话说，我们不需要回退文本串的搜索位置），这加快了搜索速率。

同样的，当搜索到下面情况时，文本串中的字符 “C” 和模式串中的字符 “D” 不匹配，利用已知的信息，我们右移模式串，不回退搜索位置，继续去查找匹配。

最终，查找成功。

简单来说，文本串和模式串匹配失败时，kmp 算法并没有像 bf 算法描述中一样，将模式串右移 1 位，从头重新进行搜索，而是利用已匹配信息，不回退文本串的搜索位置，继续将模式串向后移动，减少比较次数，提高了效率。那么当匹配失败时，模式串究竟要向后移动多少位呢？

2.1 前缀函数

前缀是指从串首开始到某个位置结束的一个特殊子串。字符串 S 以 i 结尾的前缀表示为 Prefix(S,i)，也就是 Prefix(S,i)=S[0..i]。

真前缀指除了 S 本身的 S 的前缀。

后缀是指从某个位置开始到整个串末尾结束的一个特殊子串。字符串 S 的从 i 开头的后缀表示为 Suffix(S,i)，也就是 Suffix(S,i)=S[i..|S|-1]。

真后缀指除了 S 本身的 S 的后缀。

回到上文 kmp 算法匹配流程中，当文本串和模式串匹配失败时，我们右移模式串的位数是多少呢？或者说，当文本串中字符与模式串中字符匹配失败时，应该重新跟模式串中哪个字符再进行匹配呢？

上面的例子文本串中 $ 与模式串中 D 匹配失败，而由于已经匹配成功了 “ABCDAB” 这 6 个字符，我们发现可以将模式串右移 4 位再进行比较，或者说此时，当匹配至模式串第 7 个字符失败后，可以重新和模式串的第 3 个字符，也就是 “C” 进行比较，这是由于文本串中的 “AB” 恰好和模式串中的前缀 “AB” 相匹配。而且我们发现匹配失败前文本串中的 “AB” 和已匹配的模式串中的后缀 “AB” 也是相匹配的。所以实际上我们根据模式串自身的特点，就能知道匹配失败时如何去匹配新的位置。

我们定义数组 prefix，其中 prefix[i] 表示以 S.charAt(i) 为结尾的即 S[0..i] 中最长的相同真前后缀的长度。以字符串 “aabaaab” 为例：

i=0 时，子串 “a” 无真前后缀，prefix[0]=0

i=1 时，子串 “aa”，其中 [a] a 和 a[a] 最长的相同真前后缀为 a，prefix[1]=1

i=2 时，子串 “aab” 无相同的真前后缀，prefix[2]=0

i=3 时，子串 “aaba”，其中 [a] aba aab[a] 最长的相同真前后缀为 a，prefix[3]=1

i=4 时，子串 “aabaa”，其中 [aa] baa aab[aa] 最长的相同真前后缀为 aa，prefix[4]=2

i=5 时，子串 “aabaaa”，其中 [aa] baaa aaba[aa] 最长的相同真前后缀为 aa，prefix[5]=2

i=6 时，子串 “aabaaab”，其中 [aab] aaab aaba[aab] 最长的相同真前后缀为 aab，prefix[6]=3

上文匹配的 prefix 数组如下：

如何求解 prefix 呢，很容易想到一种方法是，我们使用两个 for 循环来遍历给定字符串的前缀中的真前缀和真后缀，内部去比较真前缀和真后缀是否相同。即便我们从最长的真前后缀来尝试匹配，这个方法的时间复杂度还是很高。

public static int[] getPrefix(String str){
        int[] res = new int[str.length()];
        for(int i = 1; i < res.length; ++i){
            for(int j = i; j > 0; --j){
                if (str.substring(0, j).equals(str.substring(i-j+1,i+1))){
                    res[i] = j;
                    break;
                }
            }
        }
        return res;
    }

2.2 第一个优化

我们观察下由 s[i] 至 s[i+1] 求解最长的真前后缀匹配情况变化。

// compute "ABCDA" -> compute "ABCDAB"
// A        A       <-"ABCDA"时最长前缀、后缀匹配
// AB       DA
// ABC      CDA
// ABCD     BCDA
// ->
// A        B
// AB       AB      <-"ABCDAB"时最长前缀、后缀匹配
// ABC      DAB
// ABCD     CDAB
// ABCDA    BCDAB

// compute "ABCDA" -> compute "ABCDAP"
// A        A       <-"ABCDA"时最长前缀、后缀匹配
// AB       DA
// ABC      CDA
// ABCD     BCDA
// ->
// A        P
// AB       AP
// ABC      DAP
// ABCD     CDAP
// ABCDA    BCDAP
// 无匹配

// A->AB
// 也就是说最好的情况下，以s[i]为结尾的最长的相同的真前后缀长度，一定是以s[i-1]为结尾的最大的相同的真前后缀相同的长度+1

根据上面的描述，在尝试匹配真前后缀的时候，我们可以减少循环次数。

public static int[] getPrefix1(String str){
    int[] prefix = new int[str.length()];
    prefix[0] = 0;
    for (int i = 1; i < str.length(); ++i){
        for(int j = prefix[i-1] + 1; j > 0; --j){
            if (str.substring(0, j).equals(str.substring(i-j+1, i+1))){
                prefix[i] = j;
                break;
            }
        }
    }
    return prefix;
}

考虑一种情况，计算字符串 “baabaab” 的 prefix 的时候，在计算 i=5 的时候，我们已经完成了 “baa” 的比较，当计算 i=6 的时候，我们比较前缀 “baab” 和后缀 “baab”，但是在上一次比较，我们知道前缀 “baa” 和后缀 “baa” 已经匹配了。

为了减少这种重复的匹配，我们考虑一下利用双指针来不断的去比较所指的两个字符

// if(s.charAt(i) == s.charAt(j))
//      prefix[i] = prefix[j-1] + 1;
//      or
//      prefix[i] = j + 1;
// }

具体实现如下：

public static int[] getPrefix2(String str){
    int[] prefix = new int[str.length()];
    int j = 0;
    int i = 1;
    while(i < str.length()){
        if (str.charAt(j) == str.charAt(i)){
            j++;
            prefix[i] = j;
            i++;
        }else{
            // 匹配失败时，
            while(j > 0 && !str.substring(0, j).equals(str.substring(i-j+1, i+1))){
                j--;
            }
            prefix[i] = j;
            i++;
        }
    }
    return prefix;
}

2.3 第二个优化

上面的优化是针对匹配成功时候的情况，那么匹配失败时，难道真的需要重新去枚举其他的真前后缀，来去不断的尝试匹配吗？我们观察下，匹配失败时，能否利用前面已经计算完的结果呢？

当 s[j]!=s[i] 的时候，我们是知道 s[0..j-1] 和 s[i-j..i-1] 是相同的，到这里再回想一下 prefix 数组的定义，prefix[j-1] 表示的是以 s.charAt(j-1) 字符为结尾的即 s[0..j-1] 中最长的相同真前后缀的长度，如果 prefix[j-1]=x(x!=0)，我们很容易得到 s[0..x-1] 和 s[j-x..j-1] 是相同的。

再将 s[i-j..i-1] 展开来看一下，因为我们知道 s[0..j-1] 和 s[i-j..i-1] 是相同的，所以 s[i-j..i-1] 也同样存在相同的真前后缀，即真前缀 s[i-j-x..i-j] 以及真后缀 s[i-x..i-1]，而且由于 s[0..x-1] 和 s[j-x..j-1] 是相同的，s[j-x..j-1] 和 s[i-x..i-1] 是相同的（整体相同，对应的部分也是相同的），可以容易得到 s[0..x-1] 和 s[i-x..i-1] 是相同的。

再回到原始的字符串上来观察，s[0..x-1] 正是字符串 s 的真前缀，而 s[i-x..i-1] 是以 i-1 为结尾的真后缀，由于这两部分相同，我们更新 j=x=prefix[j-1]，准确找到已经匹配的部分，继续完成后续的匹配即可。

代码实现如下：

public static int[] getPrefix4(String str){
    int[] prefix = new int[str.length()];
    int j = 0;
    int i = 1;
    while(i < str.length()){
        if (str.charAt(j) == str.charAt(i)){
            // 更新j，同时j++也正是已匹配的最大长度
            j++;
            prefix[i] = j;
            i++;
        }else if(j == 0){
            // 当str.charAt(j) != str.charAt(i) && j == 0时，后移i即可
            i++;
        }else{
            // 找到已匹配的部分，继续匹配即可
            j = prefix[j-1];
        }
    }
    return prefix;
}

2.4 求解 next

很多 kmp 算法的讲解都提到了 next 数组，那么实际上 next 数组求解和上面的 prefix 求解本质是一样的，next[i] 实际上就是以 i-1 为结尾的最长的相同真前后缀的长度。

定义 next[j] 为当 s[i] != p[j] 时，需要跳转匹配的模式串的索引，特别的当 next[0] = -1

public static int[] getNext(String str){
    int[] next = new int[str.length()+1];
    int i = 1;
    int j = 0;
    // next[0] = -1 指代匹配失败，更新文本串索引+1
    next[0] = -1;
    while(i < str.length()){
        if (j == -1 || str.charAt(i) == str.charAt(j)){
            i++;
            j++;
            next[i] = j;
        }else{
            j = next[j];
        }
    }
    return next;
}

2.5 完整代码

public static int search(String s, String p){
    int[] next = getNext(p);
    int i = 0, j = 0;
    while(i < s.length() && j < p.length()){
        if (j == -1 || s.charAt(i) == p.charAt(j)){
            i++;
            j++;
        }else{
           j = next[j];
        }
        if (j == p.length()){
            return i - j;
        }
    }
    return -1;
}

2.6 优化 next

以上面的 next 数组为例，当 i=5，匹配失败时，应该跳转 i=1 进行比较，但是我们知道 s[5]=s[1]="B"，这样匹配下去也是必定会失败的，基于这一点，还可以简单优化下 next 数组的求解过程。

public static int[] getNext1(String str){
    int[] next = new int[str.length()+1];
    int i = 1;
    int j = 0;
    next[0] = -1;
    while(i < str.length()){
        if (j == -1 || str.charAt(i) == str.charAt(j)){
            i++;
            j++;
            if (i < str.length() && str.charAt(i) != str.charAt(j)){
                next[i] = j;
            }else{
                // 如果相同，根据next[j]跳转即可
                next[i] = next[j];
            }
        }else{
            j = next[j];
        }
    }
    return next;
}

三、其他算法

这一部分，介绍几种其他字符串搜索的算法

3.1 BM

1977 年，德克萨斯大学的 Robert S.Boyer 教授和 J StrotherMoore 教授发明了一种新的字符串匹配算法：Boyer-Moore 算法，简称 BM 算法。BM 算法的基本思想是通过后缀匹配获得比前缀匹配更多的信息来实现更快的字符跳转。

通常我们都是从左至右去匹配文本串和模式串的，下面我们从右至左尝试匹配并观察下。文本串中的字符 “S”，在模式串中未出现，那么我们是不是可以跳过多余的匹配，不用去考虑模式串从文本串中第 1 个、第 2 个、第 m 个字符进行匹配了。可以直接将模式串向后滑动 m 个字符进行匹配。

继续观察下面匹配失败的情况，我们可以发现，模式串后三个字符 “E”、“L”、“P” 一定无法和文本串中的字符 “M” 进行匹配。换句话说，直到移动到模式串中最右边的 “M”(如果存在的话) 之前，都是无法匹配成功的。基于这个观察，我们可以直接向后移动模式串，使最右边出现的 “M” 和文本串中的 “M” 对齐，再去继续匹配。

总结：1.当出现失配字符时（文本串的字符），如果模式串不存在该字符，则将模式串右移至失配字符的右边。

2.如果模式串中存在该字符，将模式串中该字符在最右边的位置，和文本串的失配字符对齐。

我们再观察下面的情况，我们发现文本串中字符 “A” 和模式串中的字符 “B” 匹配失败，此时已匹配的后缀 “AB” 我们可以在模式串中找到同样的子串 “AB”，我们完全可以向后移动模式串，将两个串中的 “AB” 来对齐，再继续匹配。

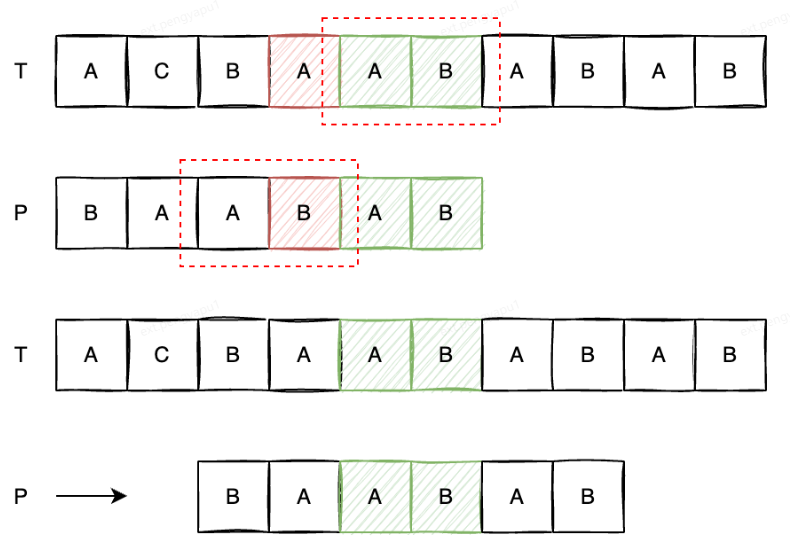
再观察下面这种情况，已经匹配的后缀 “CBAB” 我们无法在模式串中找到同样的部分，难道就没有办法加快匹配了吗？我们以匹配的字符串 “CBAB” 中的几个真后缀 “BAB”、“AB”、“B”，其中 “AB” 作为前缀出现在了模式串中，那我们可以后移模式串，将文本串中的后缀 “AB” 和模式串中的前缀 “AB” 对齐，从而继续进行匹配。

为什么已匹配的字符的真后缀必须要和模式串中的前缀匹配才可以移动呢？我们可以看下面这个例子。已匹配的 “CBAB” 中的真后缀 “AB”，在模式串中是存在的（非前缀），那我们向后移动模式串把这两部分对齐继续匹配如何呢？这样做看似合理，但实际上却是一个无效的匹配位置。很明显，因为文本串中 “AB” 前的字符和模式串中 “AB” 前的字符一定是不匹配的，否则我们是可以找到一个比 “AB” 更长的匹配，且这个匹配的一定是模式串中的前缀，这就符合我们上面说的情况了。所以当没有能够匹配上合理后缀这种情况出现时，正确的移动是将模式串向后移动 m 位。

总结：1.当模式串中有子串和已匹配后缀完全相同，则将最靠右的那个子串移动到后缀的位置继续进行匹配。

2.如果不存在和已匹配后缀完全匹配的子串，则在已匹配后缀中找到最长的真后缀，且是模式串的前缀 (t[m-s…m]=P[0…s])

3.如果完全不存在和好后缀匹配的子串，则右移整个模式串。

BM 算法在实际匹配时，考虑上面两种策略，当匹配失败发生时，会选择能够移动的最大的距离，来去移动模式串，从而加速匹配。实际情况，失配字符移动策略已经能很好的加速匹配过程，因为模式串本身字符数量是要少于文本串的，Quick Search algorithm（Sunday）正是利用这一策略的算法（有些许不同），或者说是一种简化版的 BM 算法。

3.2 Sunday

Sunday 算法是 Daniel M.Sunday 于 1990 年提出的字符串模式匹配。其效率在匹配随机的字符串时比其他匹配算法还要更快。Sunday 算法的实现可比 KMP，BM 的实现容易的多。

Sunday 算法思想跟 BM 算法很相似，在匹配失败时关注的是文本串中参加匹配的最末位字符的下一位字符。如果该字符没有在模式串中出现则直接跳过，即移动步长= 模式串长度 +1；否则，同 BM 算法一样其移动步长=模式串中最右端的该字符到末尾的距离 +1。

文本串 T 中字符 “c” 和模式串中的字符 “d” 不匹配。我们观察文本串参与匹配的末位的下一个字符 “e”，可以知道 “e” 没有出现在模式串中。于是移动模式串长度 +1。

继续匹配，我们发现文本串 T 中字符 “a” 和模式串中的字符 “d” 不匹配。我们观察文本串参与匹配的末位的下一个字符 “a”，可以知道 “a” 出现在模式串中（最右的位置）。于是移动模式串该字符到末尾的距离 +1。

3.3 Rabin-Karp

Rabin-Karp 算法，由 Richard M. Karp 和 Michael O. Rabin 在 1987 年发表，它也是用来解决多模式串匹配问题的。该算法实现方式与上述的字符匹配不同，首先是计算两个字符串的哈希值，然后通过比较这两个哈希值的大小来判断是否出现匹配。

为了帮助更好的解决字符串匹配问题，哈希函数应该具有以下属性:

1.高效的、可计算的

2.更好的识别字符串

3.在计算 hash(y[j+1 ..j+m]) 应该可以容易的从 hash(y[j..j+m-1]) 和 y[j+m] 中得到结果，即 hash(y[j+1 ..j+m])=rehash(y[j],y[j+m],hash(y[j..j+m-1])

我们定义 hash 函数如下：

hash(w[0 ..m-1])=(w[0]*2^{m-1+w[1]*2^{m-2+···+w[m-1]*2⁰⁾}} mod q

由于计算的 hash 值可能会很大，所以需要取模操作，q 最好选取一个比较大的数，且是一个质数，w[i] 表示 y[i] 对应的 ASCII 码。

hash(w[1..m])=rehash(w[0],w[m],hash(w[0..m-1]))

rehash(a,b,h)= ((h-a*2^m-1)*2+b) mod q

匹配过程中，不断滑动窗口来计算文本串的 hash 值和模式串的是否相同，当出现相同时，还需要再检查一遍字符串是否真正相同，因为会出现哈希碰撞的情况。

3.4 Shift-and/or

Shift-and 算法的总体思路是把模式串预处理成一种特殊编码形式，然后根据这种编码形式去逐位匹配文本串。

首先对模式串进行预处理，利用二进制数位进行编码。如果模式串为 “abac”，a 出现在第 0 位和第 2 位，那么则可以保存 a 的信息为 5(二进制为 0101)，同样的，我们把模式串出现的所有字符均用这种方式编码，并保存起来。

对于每一位文本串字符，我们定义一个对应的状态码数字 P，当 P[i]=1 时，则表示以这一位文本串为末尾时，能和模式串的第 0 位到第 i 位的字符能完全匹配。我们看一下具体的匹配过程。

文本串 “aeabcaabace” 和模式串 “abac”，初始化 P=0，遍历文本串中的每一个字符，同时根据存储的字符编码信息，来更新匹配结果，也就是状态码 P。

在第一次计算完成后，状态码 P=0001，根据我们上面的定义，P[0]=1 即表示以这一位文本串为末尾，模式串中的第 0 位到第 0 位的字符是匹配的。

进行完一次匹配后，P 左移一位，将第 0 位置 1，同时和对应字符的编码进行&操作（即尝试匹配该字符），更新状态码 P。

可以看到当状态码 P=0101 时，P[2]=1 表示当前字符匹配了模式串 p[0..2]=“aba”，P[0]=1 表示当前字符匹配了模式串 p[0..0]=“a”，也就是说，状态码 P 是能够存储多种部分匹配的结果。

继续匹配

当 P=1000 时，也就是说 P[3]=1 即匹配模式串 p[0...3]=“abac”，正好找到了一个对应的匹配，而我们也可以根据此条件来判断是否已经找到了匹配。

Shift-and 使用的二进制信息来编码模式串，使用位运算&来达到并行匹配字符串，利用状态码 P 来保存当前位的匹配结果。可以观察出算法的时间复杂度很低，如果模式串的长度不超过机器字长，其效率是非常高的。

Shift-or 在这里就不多做介绍了，其原理和 Shift-and 类似，只不过 Shift-or 使用 0 来标识存在，同时使用｜来代替&进行状态码的计算。

新手区 一些常见的字符串匹配算法

新手区 一些常见的字符串匹配算法

一、简介

1.1 Background

1.2 Brute force

二、KMP

2.1 前缀函数

2.2 第一个优化

2.3 第二个优化

2.4 求解 next

2.5 完整代码

2.6 优化 next

三、其他算法

3.1 BM

3.2 Sunday

3.3 Rabin-Karp

3.4 Shift-and/or

新手区一些常见的字符串匹配算法

新手区一些常见的字符串匹配算法