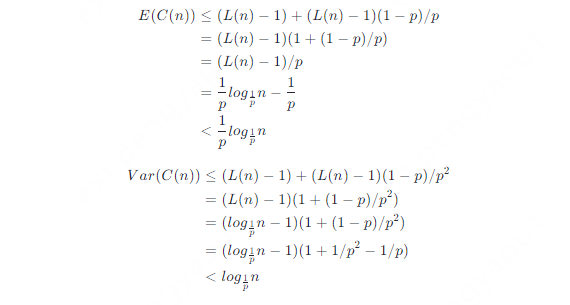数据测试跳跃表数据结构与算法分析

京东云开发者 · 2023年01月16日 · 3103 次阅读

作者：京东物流纪卓志

目前市面上充斥着大量关于跳跃表结构与 Redis 的源码解析，但是经过长期观察后发现大都只是在停留在代码的表面，而没有系统性地介绍跳跃表的由来以及各种常量的由来。作为一种概率数据结构，理解各种常量的由来可以更好地进行变化并应用到高性能功能开发中。本文没有重复地以对现有优秀实现进行代码分析，而是通过对跳跃表进行了系统性地介绍与形式化分析，并给出了在特定场景下的跳跃表扩展方式，方便读者更好地理解跳跃表数据结构。

跳跃表 [1,2,3] 是一种用于在大多数应用程序中取代平衡树的概率数据结构。跳跃表拥有与平衡树相同的期望时间上界，并且更简单、更快、是用更少的空间。在查找与列表的线性操作上，比平衡树更快，并且更简单。

概率平衡也可以被用在基于树的数据结构 [4] 上，例如树堆（Treap）。与平衡二叉树相同，跳跃表也实现了以下两种操作

通过搜索引用 [5]，可以保证从任意元素开始，搜索到在列表中间隔为 k 的元素的任意期望时间是 O(logk)
实现线性表的常规操作（例如将元素插入到列表第 k 个元素后面）

这几种操作在平衡树中也可以实现，但是在跳跃表中实现起来更简单而且非常的快，并且通常情况下很难在平衡树中直接实现（树的线索化可以实现与链表相同的效果，但是这使得实现变得更加复杂 [6]）

预览

最简单的支持查找的数据结构可能就是链表。Figure.1 是一个简单的链表。在链表中执行一次查找的时间正比于必须考查的节点个数，这个个数最多是 N。

Figure.1 Linked List

Figure.2 表示一个链表，在该链表中，每个一个节点就有一个附加的指针指向它在表中的前两个位置上的节点。正因为这个前向指针，在最坏情况下最多考查⌈N/2⌉+1 个节点。

Figure.2 Linked List with fingers to the 2nd forward elements

Figure.3 将这种想法扩展，每个序数是 4 的倍数的节点都有一个指针指向下一个序数为 4 的倍数的节点。只有⌈N/4⌉+2 个节点被考查。

Figure.3 Linked List with fingers to the 4th forward elements

这种跳跃幅度的一般情况如 Figure.4 所示。每个 2i 节点就有一个指针指向下一个 2i 节点，前向指针的间隔最大为 N/2。可以证明总的指针最大不会超过 2N（见空间复杂度分析），但现在在一次查找中最多考查⌈logN⌉个节点。这意味着一次查找中总的时间消耗为 O(logN)，也就是说在这种数据结构中的查找基本等同于二分查找（binary search）。

Figure.4 Linked List with fingers to the 2ith forward elements

在这种数据结构中，每个元素都由一个节点表示。每个节点都有一个高度（height）或级别（level），表示节点所拥有的前向指针数量。每个节点的第 i 个前向指针指向下一个级别为 i 或更高的节点。

在前面描述的数据结构中，每个节点的级别都是与元素数量有关的，当插入或删除时需要对数据结构进行调整来满足这样的约束，这是很呆板且低效的。为此，可以将每个 2i 节点就有一个指针指向下一个 2i 节点的限制去掉，当新元素插入时为每个新节点分配一个随机的级别而不用考虑数据结构的元素数量。

Figure.5 Skip List

数据结构

到此为止，已经得到了所有让链表支持快速查找的充要条件，而这种形式的数据结构就是跳跃表。接下来将会使用更正规的方式来定义跳跃表

所有元素在跳跃表中都是由一个节点表示。
每个节点都有一个高度或级别，有时候也可以称之为阶（step），节点的级别是一个与元素总数无关的随机数。规定 NULL 的级别是∞。
每个级别为 k 的节点都有 k 个前向指针，且第 i 个前向指针指向下一个级别为 i 或更高的节点。
每个节点的级别都不会超过一个明确的常量 MaxLevel。整个跳跃表的级别是所有节点的级别的最高值。如果跳跃表是空的，那么跳跃表的级别就是 1。
存在一个头节点 head，它的级别是 MaxLevel，所有高于跳跃表的级别的前向指针都指向 NULL。

稍后将会提到，节点的查找过程是在头节点从最高级别的指针开始，沿着这个级别一直走，直到找到大于正在寻找的节点的下一个节点（或者是 NULL），在此过程中除了头节点外并没有使用到每个节点的级别，因此每个节点无需存储节点的级别。

在跳跃表中，级别为 1 的前向指针与原始的链表结构中 next 指针的作用完全相同，因此跳跃表支持所有链表支持的算法。

对应到高级语言中的结构定义如下所示（后续所有代码示例都将使用 C 语言描述）

#define SKIP_LIST_KEY_TYPE     int
#define SKIP_LIST_VALUE_TYPE   int
#define SKIP_LIST_MAX_LEVEL    32
#define SKIP_LIST_P            0.5

struct Node {
  SKIP_LIST_KEY_TYPE    key;
  SKIP_LIST_VALUE_TYPE  value;
  struct Node          *forwards[]; // flexible array member
};

struct SkipList {
  struct Node *head;
  int          level;
};

struct Node *CreateNode(int level) {
  struct Node *node;
  assert(level > 0);
  node = malloc(sizeof(struct Node) + sizeof(struct Node *) * level);
  return node;
}

struct SkipList *CreateSkipList() {
  struct SkipList *list;
  struct Node     *head;
  int              i;

  list = malloc(sizeof(struct SkipList));
  head = CreateNode(SKIP_LIST_MAX_LEVEL);
  for (i = 0; i < SKIP_LIST_MAX_LEVEL; i++) {
    head->forwards[i] = NULL;
  }
  list->head = head;
  list->level = 1;

  return list;
}

从前面的预览章节中，不难看出 MaxLevel 的选值影响着跳跃表的查询性能，关于 MaxLevel 的选值将会在后续章节中进行介绍。在此先将 MaxLevel 定义为 32，这对于 232 个元素的跳跃表是足够的。延续预览章节中的描述，跳跃表的概率被定义为 0.5，关于这个值的选取问题将会在后续章节中进行详细介绍。

算法

搜索

在跳跃表中进行搜索的过程，是通过 Z 字形遍历所有没有超过要寻找的目标元素的前向指针来完成的。在当前级别没有可以移动的前向指针时，将会移动到下一级别进行搜索。直到在级别为 1 的时候且没有可以移动的前向指针时停止搜索，此时直接指向的节点（级别为 1 的前向指针）就是包含目标元素的节点（如果目标元素在列表中的话）。在 Figure.6 中展示了在跳跃表中搜索元素 17 的过程。

Figure.6 A search path to find element 17 in Skip List

整个过程的示例代码如下所示，因为高级语言中的数组下标从 0 开始，因此 forwards[0] 表示节点的级别为 1 的前向指针，依此类推

struct Node *SkipListSearch(struct SkipList *list, SKIP_LIST_KEY_TYPE target) {
  struct Node *current;
  int          i;

  current = list->head;
  for (i = list->level - 1; i >= 0; i--) {
    while (current->forwards[i] && current->forwards[i]->key < target) {
      current = current->forwards[i];
    }
  }

  current = current->forwards[0];
  if (current->key == target) {
    return current;
  } else {
    return NULL;
  }
}

插入和删除

在插入和删除节点的过程中，需要执行和搜索相同的逻辑。在搜索的基础上，需要维护一个名为 update 的向量，它维护的是搜索过程中跳跃表每个级别上遍历到的最右侧的值，表示插入或删除的节点的左侧直接直接指向它的节点，用于在插入或删除后调整节点所在所有级别的前向指针（与朴素的链表节点插入或删除的过程相同）。

当新插入节点的级别超过当前跳跃表的级别时，需要增加跳跃表的级别并将 update 向量中对应级别的节点修改为 head 节点。

Figure.7 和 Figure.8 展示了在跳跃表中插入元素 16 的过程。首先，在 Figure.7 中执行与搜索相同的查询过程，在每个级别遍历到的最后一个元素在对应层级的前向指针被标记为灰色，表示稍后将会对齐进行调整。接下来在 Figure.8 中，在元素为 13 的节点后插入元素 16，元素 16 对应的节点的级别是 5，这比跳跃表当前级别要高，因此需要增加跳跃表的级别到 5，并将 head 节点对应级别的前向指针标记为灰色。Figure.8 中所有虚线部分都表示调整后的效果。

Figure.7 Search path for inserting element 16

Figure.8 Insert element 16 and adjust forward pointers

struct Node *SkipListInsert(struct SkipList *list, SKIP_LIST_KEY_TYPE key, SKIP_LIST_VALUE_TYPE value) {
  struct Node *update[SKIP_LIST_MAX_LEVEL];
  struct Node *current;
  int          i;
  int          level;

  current = list->head;
  for (i = list->level - 1; i >= 0; i--) {
    while (current->forwards[i] && current->forwards[i]->key < target) {
      current = current->forwards[i];
    }
    update[i] = current;
  }

  current = current->forwards[0];
  if (current->key == target) {
    current->value = value;
    return current;
  }

  level = SkipListRandomLevel();
  if (level > list->level) {
    for (i = list->level; i < level; i++) {
      update[i] = list->header;
    }
  }

  current = CreateNode(level);
  current->key = key;
  current->value = value;

  for (i = 0; i < level; i++) {
    current->forwards[i] = update[i]->forwards[i];
    update[i]->forwards[i] = current;
  }

  return current;
}

在删除节点后，如果删除的节点是跳跃表中级别最大的节点，那么需要降低跳跃表的级别。

Figure.9 和 Figure.10 展示了在跳跃表中删除元素 19 的过程。首先，在 Figure.9 中执行与搜索相同的查询过程，在每个级别遍历到的最后一个元素在对应层级的前向指针被标记为灰色，表示稍后将会对齐进行调整。接下来在 Figure.10 中，首先通过调整前向指针将元素 19 对应的节点从跳跃表中卸载，因为元素 19 对应的节点是级别最高的节点，因此将其从跳跃表中移除后需要调整跳跃表的级别。Figure.10 中所有虚线部分都表示调整后的效果。

Figure.9 Search path for deleting element 19

Figure.10 Delete element 19 and adjust forward pointers

struct Node *SkipListDelete(struct SkipList *list, SKIP_LIST_KEY_TYPE key) {
  struct Node *update[SKIP_LIST_MAX_LEVEL];
  struct Node *current;
  int          i;

  current = list->head;
  for (i = list->level - 1; i >= 0; i--) {
    while (current->forwards[i] && current->forwards[i]->key < key) {
      current = current->forwards[i];
    }
    update[i] = current;
  }

  current = current->forwards[0];
  if (current && current->key == key) {
    for (i = 0; i < list->level; i++) {
      if (update[i]->forwards[i] == current) {
        update[i]->forwards[i] = current->forwards[i];
      } else {
        break;
      }
    }

    while (list->level > 1 && list->head->forwards[list->level - 1] == NULL) {
      list->level--;
    }
  }

  return current;
}

生成随机级别

int SkipListRandomLevel() {
  int level;
  level = 1;
  while (random() < RAND_MAX * SKIP_LIST_P && level <= SKIP_LIST_MAX_LEVEL) {
    level++;
  }
  return level;
}

以下表格为按上面算法执行 232 次后，所生成的随机级别的分布情况。

1	2	3	4	5	6	7	8
2147540777	1073690199	536842769	268443025	134218607	67116853	33563644	16774262
9	10	11	12	13	14	15	16
8387857	4193114	2098160	1049903	523316	262056	131455	65943
17	18	19	20	21	22	23	24
32611	16396	8227	4053	2046	1036	492	249
25	26	27	28	29	30	31	32
121	55	34	16	7	9	2	1

MaxLevel 的选择

在 Figure.4 中曾给出过对于 10 个元素的跳跃表最理想的分布情况，其中 5 个节点的级别是 1，3 个节点的级别是 2，1 个节点的级别是 3，1 个节点的级别是 4。

这引申出一个问题：既然相同元素数量下，跳跃表的级别不同会有不同的性能，那么跳跃表的级别为多少才合适？

分析

空间复杂度分析

前面提到过，分数 p 代表节点同时带有第 i 层前向指针和第 i+1 层前向指针的概率，而每个节点的级别最少是 1，因此级别为 i 的前向指针数为 npi−1。定义 S(n) 表示所有前向指针的总量，由等比数列求和公式可得

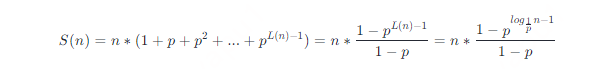
对 S(n) 求极限，有

易证，这是一个关于 p 的单调递增函数，因此 p 的值越大，跳跃表中前向指针的总数越多。因为 1−p 是已知的常数，所以说跳跃表的空间复杂度是 O(n)。

时间复杂度分析

非形式化分析

形式化分析

延续分数 p 代表节点同时带有第 i 层前向指针和第 i+1 层前向指针的概率的定义，考虑反方向分析搜索路径。

搜索的路径总是小于必须执行的比较的次数的。首先需要考查从级别 1（在搜索到元素前遍历的最后一个节点）爬升到级别 L(n) 所需要反向跟踪的指针数量。虽然在搜索时可以确定每个节点的级别都是已知且确定的，在这里仍认为只有当整个搜索路径都被反向追踪后才能被确定，并且在爬升到级别 L(n) 之前都不会接触到 head 节点。

在爬升过程中任何特定的点，都认为是在元素 x 的第 i 个前向指针，并且不知道元素 x 左侧所有元素的级别或元素 x 的级别，但是可以知道元素 x 的级别至少是 i。元素 x 的级别大于 i 的概率是 p，可以通过考虑视认为这个反向爬升的过程是一系列由成功的爬升到更高级别或失败地向左移动的随机独立实验。

在爬升到级别 L(n) 过程中，向左移动的次数等于在连续随机试验中第 L(n)−1 次成功前的失败的次数，这符合负二项分布。期望的向上移动次数一定是 L(n)−1。因此可以得到无限列表中爬升到 L(n) 的代价 C C=prob(L(n)−1)+NB(L(n)−1,p) 列表长度无限大是一个悲观的假设。当反向爬升的过程中接触到 head 节点时，可以直接向上爬升而不需要任何向左移动。因此可以得到 n 个元素列表中爬升到 L(n) 的代价 C(n)

C(n)≤probC=prob(L(n)−1)+NB(L(n)−1,p)

因此 n 个元素列表中爬升到 L(n) 的代价 C(n) 的数学期望和方差为

因为 1/p 是已知常数，因此跳跃表的搜索、插入和删除的时间复杂度都是 O(logn)。

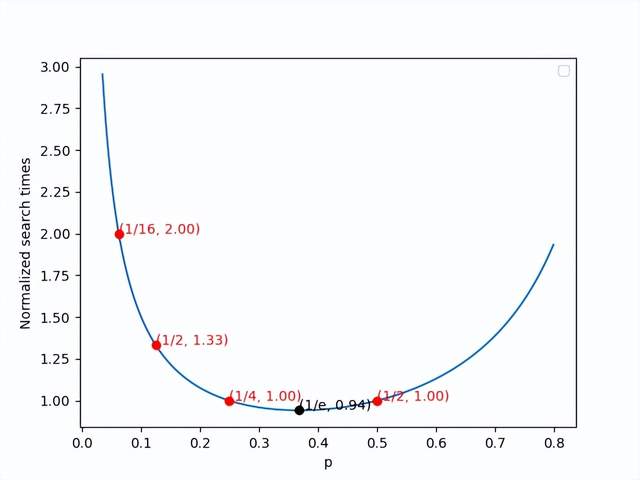
P 的选择

Figure.11 Normalized search times

扩展

快速随机访问

#define SKIP_LIST_KEY_TYPE     int
#define SKIP_LIST_VALUE_TYPE   int
#define SKIP_LIST_MAX_LEVEL    32
#define SKIP_LIST_P            0.5

struct Node; // forward definition

struct Forward {
  struct Node *forward;
  int          span;
}

struct Node {
  SKIP_LIST_KEY_TYPE    key;
  SKIP_LIST_VALUE_TYPE  value;
  struct Forward        forwards[]; // flexible array member
};

struct SkipList {
  struct Node *head;
  int          level;
  int          length;
};

struct Node *CreateNode(int level) {
  struct Node *node;
  assert(level > 0);
  node = malloc(sizeof(struct Node) + sizeof(struct Forward) * level);
  return node;
}

struct SkipList *CreateSkipList() {
  struct SkipList *list;
  struct Node     *head;
  int              i;

  list = malloc(sizeof(struct SkipList));
  head = CreateNode(SKIP_LIST_MAX_LEVEL);
  for (i = 0; i < SKIP_LIST_MAX_LEVEL; i++) {
    head->forwards[i].forward = NULL;
    head->forwards[i].span = 0;
  }

  list->head = head;
  list->level = 1;

  return list;
}

接下来需要修改插入和删除操作，来保证在跳跃表修改后跨度的数据完整性。

需要注意的是，在插入过程中需要使用 indices 记录在每个层级遍历到的最后一个元素的位置，这样通过做简单的减法操作就可以知道每个层级遍历到的最后一个元素到新插入节点的跨度。

struct Node *SkipListInsert(struct SkipList *list, SKIP_LIST_KEY_TYPE key, SKIP_LIST_VALUE_TYPE value) {
  struct Node *update[SKIP_LIST_MAX_LEVEL];
  struct Node *current;
  int          indices[SKIP_LIST_MAX_LEVEL];
  int          i;
  int          level;

  current = list->head;
  for (i = list->level - 1; i >= 0; i--) {
    if (i == list->level - 1) {
      indices[i] = 0;
    } else {
      indices[i] = indices[i + 1];
    }

    while (current->forwards[i].forward && current->forwards[i].forward->key < target) {
      indices[i] += current->forwards[i].span;
      current = current->forwards[i].forward;
    }
    update[i] = current;
  }

  current = current->forwards[0].forward;
  if (current->key == target) {
    current->value = value;
    return current;
  }

  level = SkipListRandomLevel();
  if (level > list->level) {
    for (i = list->level; i < level; i++) {
      indices[i] = 0;
      update[i] = list->header;
      update[i]->forwards[i].span = list->length;
    }
  }

  current = CreateNode(level);
  current->key = key;
  current->value = value;

  for (i = 0; i < level; i++) {
    current->forwards[i].forward = update[i]->forwards[i].forward;
    update[i]->forwards[i].forward = current;
    current->forwards[i].span = update[i]->forwards[i].span - (indices[0] - indices[i]);
    update[i]->forwards[i].span = (indices[0] - indices[i]) + 1;
  }

  list.length++;

  return current;
}

struct Node *SkipListDelete(struct SkipList *list, SKIP_LIST_KEY_TYPE key) {
  struct Node *update[SKIP_LIST_MAX_LEVEL];
  struct Node *current;
  int          i;

  current = list->head;
  for (i = list->level - 1; i >= 0; i--) {
    while (current->forwards[i].forward && current->forwards[i].forward->key < key) {
      current = current->forwards[i].forward;
    }
    update[i] = current;
  }

  current = current->forwards[0].forward;
  if (current && current->key == key) {
    for (i = 0; i < list->level; i++) {
      if (update[i]->forwards[i].forward == current) {
        update[i]->forwards[i].forward = current->forwards[i];
        update[i]->forwards[i].span += current->forwards[i].span - 1;
      } else {
        break;
      }
    }

    while (list->level > 1 && list->head->forwards[list->level - 1] == NULL) {
      list->level--;
    }
  }

  return current;
}

当实现了快速随机访问之后，通过简单的指针操作即可实现区间查询功能。

参考文献

Pugh, W. (1989). A skip list cookbook. Tech. Rep. CS-TR-2286.1, Dept. of Computer Science, Univ. of Maryland, College Park, MD [July 1989]
Pugh, W. (1989). Skip lists: A probabilistic alternative to balanced trees. Lecture Notes in Computer Science, 437–449. https://doi.org/10.1007/3-540-51542-9_36
Weiss, M. A. (1996).Data Structures and Algorithm Analysis in C (2nd Edition)(2nd ed.). Pearson.
Aragon, Cecilia & Seidel, Raimund. (1989). Randomized Search Trees. 540-545. 10.1109/SFCS.1989.63531.
Wikipedia contributors. (2022b, November 22).Finger search. Wikipedia. https://en.wikipedia.org/wiki/Finger_search
Wikipedia contributors. (2022a, October 24).Threaded binary tree. Wikipedia. https://en.wikipedia.org/wiki/Threaded_binary_tree
Wikipedia contributors. (2023, January 4).Negative binomial distribution. Wikipedia. https://en.wikipedia.org/wiki/Negative_binomial_distribution
Redis contributors.Redis ordered set implementation. GitHub. https://github.com/redis/redis

后续工作

确定性跳跃表
无锁并发安全跳跃表

因文章展示完整性需要，所以部分公式内容采用截图上传，排版不当之处还望包涵。

暂无回复。

需要登录后方可回复, 如果你还没有账号请点击这里注册。

数据测试 跳跃表数据结构与算法分析

数据测试 跳跃表数据结构与算法分析

预览

数据结构

算法

搜索

插入和删除

生成随机级别

MaxLevel 的选择

分析

空间复杂度分析

时间复杂度分析

非形式化分析

形式化分析

P 的选择

扩展

快速随机访问

参考文献

后续工作

因文章展示完整性需要，所以部分公式内容采用截图上传，排版不当之处还望包涵。

数据测试跳跃表数据结构与算法分析

数据测试跳跃表数据结构与算法分析