最近在学习 TensorFlow,学习方式是看 TensorFlow 中文社区的完整教程http://www.tensorfly.cn/tfdoc/tutorials/overview.html ,刚看到 MNIST 入门就看的我有点绝望,一篇文章http://www.tensorfly.cn/tfdoc/tutorials/mnist_beginners.html 看了三遍都没看懂,感受到满满的绝望感,在这里记录学习的过程,希望有一天能开窍。
一、什么是 MNIST
MNIST database,全称 Mixed National Institute of Standards and Technology database,是一个手写数字的数据库,通常用于训练各种图像系统。MNIST 共包括两部分:60000 张图片的训练数据集(来源于美国人口普查局)和 10000 张图片的测试数据集(来自美国高中生),其中每张图片大小都是 28 像素 *28 像素,范围为 0~9。可以从 MNIST 官网http://yann.lecun.com/exdb/mnist/ 下载下列四个文件,或者执行 input_data.py(源码见https://testerhome.com/topics/18906 )下载文件。
| 文件 | 内容 |
|---|---|
| train-images-idx3-ubyte.gz | 训练集图片 - 55000 张 训练图片, 5000 张 验证图片 |
| train-labels-idx1-ubyte.gz | 训练集图片对应的数字标签 |
| t10k-images-idx3-ubyte.gz | 测试集图片 - 10000 张 图片 |
| t10k-labels-idx1-ubyte.gz | 测试集图片对应的数字标签 |
二、softmax 回归
softmax 回归 (softmax regression),多项逻辑回归的其中一种,是一种推广逻辑回归的分类方法。softmax 回归主要用于多类问题,即具有两个以上(当分类数量等于 2 时,softmax 回归与逻辑回归时一致的)可能的离散结果。softmax 回归使用 softmax 函数使得概率分布总和为 1 ,因此用来给不同的对象分配概率,是训练模型的最后一步。举例来说,我们的模型可能推测一张包含 9 的图片代表数字 9 的概率是 80% 但是判断它是 8 的概率是 5%(因为 8 和 9 都有上半部分的小圆),然后给予它代表其他数字的概率更小的值。
三、如何判断图片属于某个特定数字
判断一张给定图片属于某个特定数字类的证据(evidence),这属于 softmax 的第一步。引入权值的概念,每一张图片大小都是 28 像素 *28 像素。如果能通过这个图片里的像素推断图片属于 0~9 之间的任何一个数,则定义权值为负数;如果不能通过像素推断出为某一个数,则定义权值为正数。由于图片中可能存在干扰,加一个额外的偏执量(bias)。因此证据(evidence)的表达式为:

softmax 函数可以把这些证据转换成概率 y:
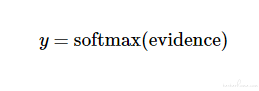
四、实现回归模型
# 导入TensorFlow
import tensorflow as tf
'''x不是一个特定的值,而是一个占位符placeholder
我们希望能够输入任意数量的MNIST图像,每一张图展平成784维的向量。
我们用2维的浮点数张量来表示这些图,这个张量的形状是[None,784 ]。(这里的None表示此张量的第一个维度可以是任何长度的。)'''
x = tf.placeholder("float", [None, 784])
'''模型参数,可以用Variable表示, 一个Variable代表一个可修改的张量
在这里,我们都用全为零的张量来初始化W和b
W的维度是[784,10],因为我们想要用784维的图片向量乘以它以得到一个10维的证据值向量,每一位对应不同数字类
b的形状是[10],所以我们可以直接把它加到输出上面'''
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
'''实现模型
我们用tf.matmul(X,W)表示x乘以W,对应之前等式里面的Wx,这里x是一个2维张量拥有多个输入
然后再加上b,把和输入到tf.nn.softmax函数里面'''
y = tf.nn.softmax(tf.matmul(x, W) + b)
MNIST 图片的大小是 28*28=784 个像素,所以 x 为 784 个节点。
五、交叉熵
交叉熵(cross-entropy),softmax 使用的成本函数,用于评估两个概率分布有多接近。如果两个概率分布很接近,则交叉熵的结果趋近于 0;如果两个概率分布的差距很大,则交叉熵的结果趋近于 1。训练模型追求的目的是,最小化成本或损失这一指标,也就是预测的概率接近真实概率。交叉熵的定义如下:

六、反向传播算法
反向传播算法(backpropagation algorithm,缩写为 BP)是 “误差反向传播” 的简称,是一种用来训练人工神经的常见算法,通常与最优化算法结合使用。其本质就是对于每一个训练实例,将它传入神经网络,计算它的输出;然后测量网络的输出误差(即期望输出和实际输出之间的差异),并计算出上一个隐藏层中各神经元为该输出结果贡献了多少的误差;反复一直从后一层计算到前一层,直到算法到达初始的输入层为止。此反向传递过程有效地测量网络中所有连接权重的误差梯度,最后通过在每一个隐藏层中应用最优化算法来优化该层的参数(反向传播算法的名称也因此而来)。
七、梯度下降算法
梯度下降算法(gradient descent algorithm)是个一阶最优化算法,通常叫做最速下降法。梯度下降过程可以比作下山的过程:
我们在一座山的山顶被困,想下到山底,但由于大雾无法看清道路,因此无法确定下山的道路。需要找个方法来帮助自己下山,方法就是:以当前所占的位置为原点,寻找倾斜度最大的坡,然后往下走一步(每走一步的距离称为步长)到相对的最低点。每走一步(我们要控制自己的步长,步子太小下山时间太长,步长太大会错过最低点的位置),都重复寻找斜度最大的坡,直到走到山底。
可微分的函数代表这座山,山底是这个函数的最小值,斜度最大的坡就是梯度,梯度的方向为上升所以需要加一个负号,步长就是学习率。
八、训练模型
# 训练模型
import tensorflow as tf
from TensorFlow import input_data
from TensorFlow import implementation_model
x = implementation_model.x
y = implementation_model.y
# 添加一个新的占位符用于输入正确值
y_ = tf.placeholder("float", [None, 10])
'''计算交叉熵
首先,用 tf.log 计算 y 的每个元素的对数。
接下来,我们把 y_ 的每一个元素和 tf.log(y_) 的对应元素相乘。
最后,用 tf.reduce_sum 计算张量的所有元素的总和。'''
cross_entropy = -tf.reduce_sum(y_*tf.log(y))
'''梯度下降算法
以0.01的学习速率最小化交叉熵'''
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# 初始化创建的变量
init = tf.initialize_all_variables()
# 在Session里启动模型,并初始化变量
sess = tf.Session()
sess.run(init)
# 训练模型
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
由于 0~9 有 10 个数字,所以 y_为 10 个节点。