哲学

由于确定两件事是否相同在很大程度上取决于上下文，因此不可能构建一个 json diff 工具来满足所有要求。

JYCM 选择了另一种方式：使比较值变得容易。

JYCM 允许用户只需要专注于定义不同的逻辑或两个值之间的距离是多少，JYCM 将处理所有其他个比较繁琐的的工作，例如数组项匹配、忽略数组顺序、递归比较和计算相似性。

顺便说一下，JYCM 使用以下算法来匹配数组中的项目：

	精准匹配	模糊匹配
有序比较	LCS	编辑距离
无序比较	暴力	匈牙利

此外，针对 json 的渲染的部分，jycm 也自带了一个渲染器，可以方便的查看 json 的 diff 以及处理 diff 路径上的配对

参考

• 为什么没有一款能称心如意的 JSONDIFF 工具？
• deepdiff
• gojsondiff

代码仓库

• Diff 代码库
• 前端展示

前言

关于 json 的 diff 的工具和应用很多，主要来源于现在大部分的接口的结果都上 json。另外由于 json 的表达能力的强大，其他的非 json 格式数据也都可以转换成 json 的格式进行序列化，因此做好 json 的 diff 的工作对于 QA 工作相当的重要。

但是如为什么没有一款能称心如意的 JSONDIFF 工具？里说的，好的 json-diff 的库似乎真的很少。以 github 上有 1100 颗🌟到deepdiff库来说，查看他的 issue 和 PR，也有很多功能并没有完善以及相当多的 bug。

最重要的，大部分的 json-diff 的库都没有提供友好的「用户自定义」功能。由于业务场景的千差万别，单一的 diff 规则或算法几乎不可能通用。举个例子：

# 基准
left = [
    {
        "x": 92134,
        "y": 42351
    }
]
#################################
# 对比
right = [
    {
        "x": 91111,
        "y": 43333
    }
]

以上面为例，left->[0]和right->[0]是否「有差」呢？如果我们把他们解释成「某个用户的账户的可提现余额」那可能我们就说他们「有差」，并且说一个严重的 bug！而如果我们说他们是「平面坐标上两个点的坐标」，那也许我们要计算他们的欧式距离才能判断他们「有差/没差」。

因此，我们做了一个专门针对 json 的 diff 工具。这篇文章用来记录在做这个工具的调研以及实现的过程。

JSON-有差吗？

那这边以数据类型的角度整理了一下 json 的 diff 的方法和逻辑，从 wiki 上的 json 的基本数据类型如下:

JSON 的基本数据类型：

• 数值：十进制数，不能有前导 0，可以为负数，可以有小数部分。还可以用e或者E表示指数部分。不能包含非数，如 NaN。不区分整数与浮点数。JavaScript 用双精度浮点数表示所有数值。
• 字符串：以双引号""括起来的零个或多个Unicode码位。支持反斜杠开始的转义字符序列。
• 布尔值：表示为true或者false。
• 值的有序列表（array）：有序的零个或者多个值。每个值可以为任意类型。序列表使用方括号[，]括起来。元素之间用逗号,分割。形如：[value, value]
• 对象（object）：若干无序的 “键 - 值对”(key-value pairs)，其中键是数值或字符串。建议但不强制要求对象中的键是独一无二的。对象以花括号{开始，并以}结束。键 - 值对之间使用逗号分隔。键与值之间用冒号:分割。
• null 类型：值写为null

primitive 的有差吗？

所谓的 primitive 就是 string、float、int、bool 等这些类型，这些类型的 Diff 比较直观去比较即可（提供的用户自定义算子也）

object 的有差吗？

object 的 diff 的话是以 key 为唯独，分为三种操作

• 更新
• 新增 key
• 删除 key

特别需要指出「更新」的操作需要递归的去做 diff。

大概的 psuedo code 如下

def diff_dict(left, right):
    for k in all_keys:
        if k in left and k in right:
            # 这个diff跟进类型去选择具体的diff逻辑
            diff(left[k], right[k])
            continue

        if k in left:
            # 则执行「新增的逻辑」
               pass

        if k in right:
            # 则执行「删除的逻辑」
            pass

array 有差吗？

array 的 diff 是最特殊的一个，也是最复杂的一个。

可能会觉得很奇怪，这个按照 index 去比较不就好了？，比如下面的逻辑

def diff_array(left, right):
    min_len = min([len(left), len(right)]

    for i in range(min_len):
        diff(left[i], right[i])

    if min_len == len(left):
        # 则新增啦right[min_len:]这些
        pass

    if min_len == len(right):
        # 则删除了left[min_len:]这些
        pass

在实际上会有一些问题，下面的例子会有说明。

作为一个整理，以「有序、无序」和「精准、模糊」两个维度来完成对于 array 的 diff 操作，用表格来整理组合以及对应到需要用到的算法：

	精准匹配	模糊匹配
有序比较	LCS	编辑距离
无序比较	暴力	匈牙利

那么为什么要这样区分呢？

• 为什么区分有序和无序？
  • 以比较「(a,b,c),(c,b,a)」为例，在有序和无序的条件下会有截然不同的结论，因此必须分开对待
• 为什么要区分「精准」和「模糊」匹配，不能直接「模糊匹配」完成嘛？
  • 因为模糊匹配本质上是配对问题，找到一个配对的组合，使得这个配对组合的成本最小。
  • 以有序的「(a,b,c),(a,z,c)」为例：有可能因为b 和 z的成本过大而导致最终将 (a和z) 匹配在一起，这个逻辑上并不合理。

而前面所说为什么不能直接 index 去比较的问题其实也已经回答了：

• 一个是无法支持「无序」状态下的物理意义
• 另外一个使用这个方法做出来的 diff 的结果并不够完美。
  • 以对比「[a,b,c,d,e],[b,c,d,e,f]」为例
  • index 方法会得到
    • 两个数组对应位置的所有元素皆不想等
  • 更合理的结论
    • 新的数组相比旧的
      • 少了第 0 个元素a
      • 多了最后一个元素f

接下来，就以前面表格的维度分享一下场景和对应我们选择的算法（并不一定是最优解，仅供参考）；

注：以下所说的 array 中的元素「相等」或者「相似」皆是以「元素」为整体考虑即可，关于递归的实现可以参考「实现 - 递归和分数」

注：下算法皆不会涉及具体的原理，只是介绍某种算法解决的问题以及如何跟我们的场景相互匹配

有序

举个例子，如果我们要 diff 两个 list：

• LEFT = (a,b,c,d,e,f,g)
• RIGHT = (t,u,v,c,x,y,e,z)

精准匹配

这里采用的 LCS 的算法。所谓 LCS 即为「最长公共子序列」。引用自 wiki

最长公共子序列（LCS）是一个在一个序列集合中（通常为两个序列）用来查找所有序列中最长子序列的问题。这与查找最长公共子串的问题不同的地方是：子序列不需要在原序列中占用连续的位置 。

下图展示了 LCS 的计算矩阵以及如何获得 LCS。

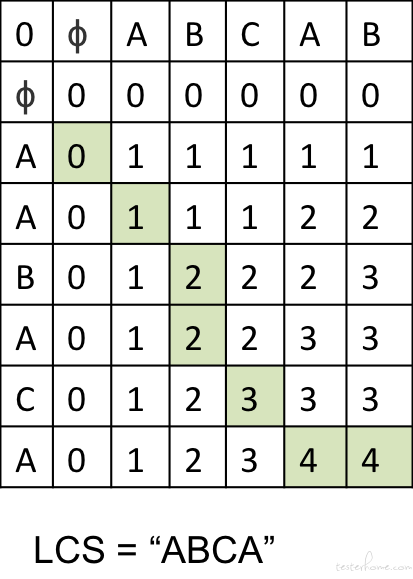
而具体以例子L1和L2来说，我们大约会得到下图中黑色连线的部分

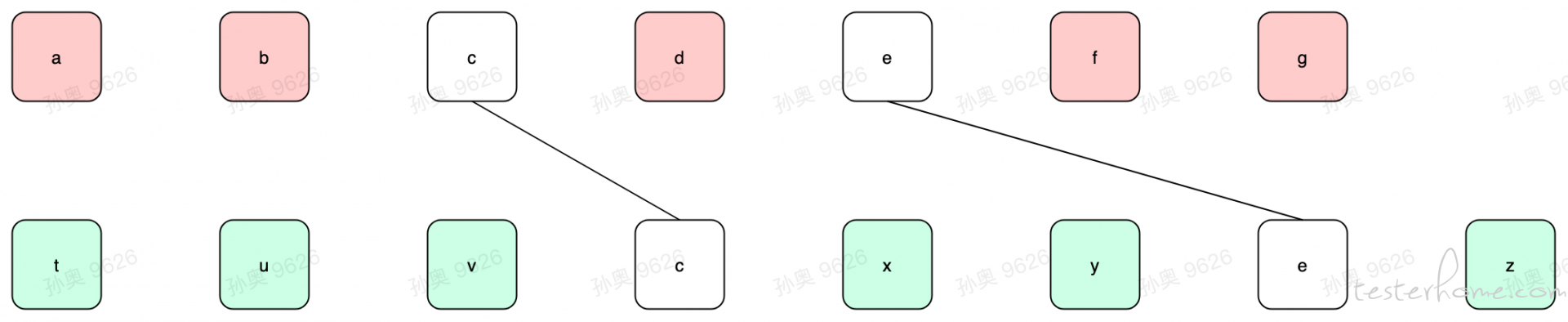
模糊匹配

剩下的为什么不能「任意去配对呢？」（规约到「无序 + 模糊匹配」？）？

• i.e. 以上图的LEFT和RIGHT来说，我们只能用「a,b」和「t,u,v」去做比较，而「a,b」是不能与「x,y」做比较的。
• 原因在于是有序，如果我们把a和x匹配了，那么在「LEFT中a在c的前面」和「RIGHT中x在c后面」就矛盾了。

因此，我们要以精准匹配的配对去切开区间，然后只有在区间内的序列才去做「模糊匹配」。

得到了比较的区间对（以上面的例子就是 ([a,b] 和 [t,u,v])、([d] 和 [x,y])、([f,g] 和 [z])），就进入了模糊匹配的阶段，我们选择类似于编辑距离的算法，先把 wiki 的定义摘录下来：

编辑距离是针对二个字符串（例如英文字）的差异程度的量化量测，量测方式是看至少需要多少次的处理才能将一个字符串变成另一个字符串。编辑距离可以用在自然语言处理中，例如拼写检查可以根据一个拼错的字和其他正确的字的编辑距离，判断哪一个（或哪几个）是比较可能的字。

• 在莱文斯坦距离中，可以删除、加入、取代字符串中的任何一个字元，也是较常用的编辑距离定义，常常提到编辑距离时，指的就是莱文斯坦距离[1]。

我们首先用「两两元素的相似度」获得一个相似度的矩阵:

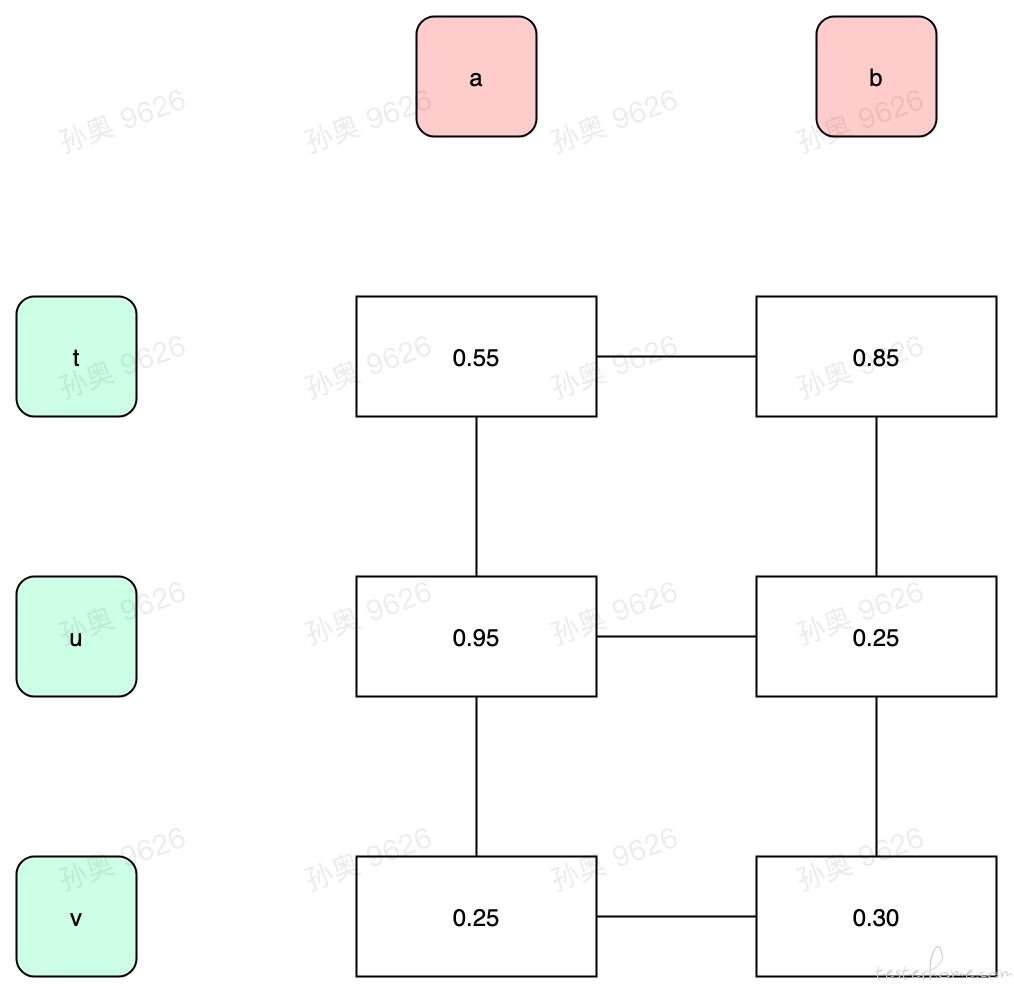
这个矩阵就是表达的就是「元素 x 变换到元素 y 的相似度，对应的其实就是更新操作的代价」，然后通过编辑距离的算法可以得到一个矩阵最后再还原成操作的序列。

下图是一个通过编辑距离的矩阵获得具体操作的示意图：

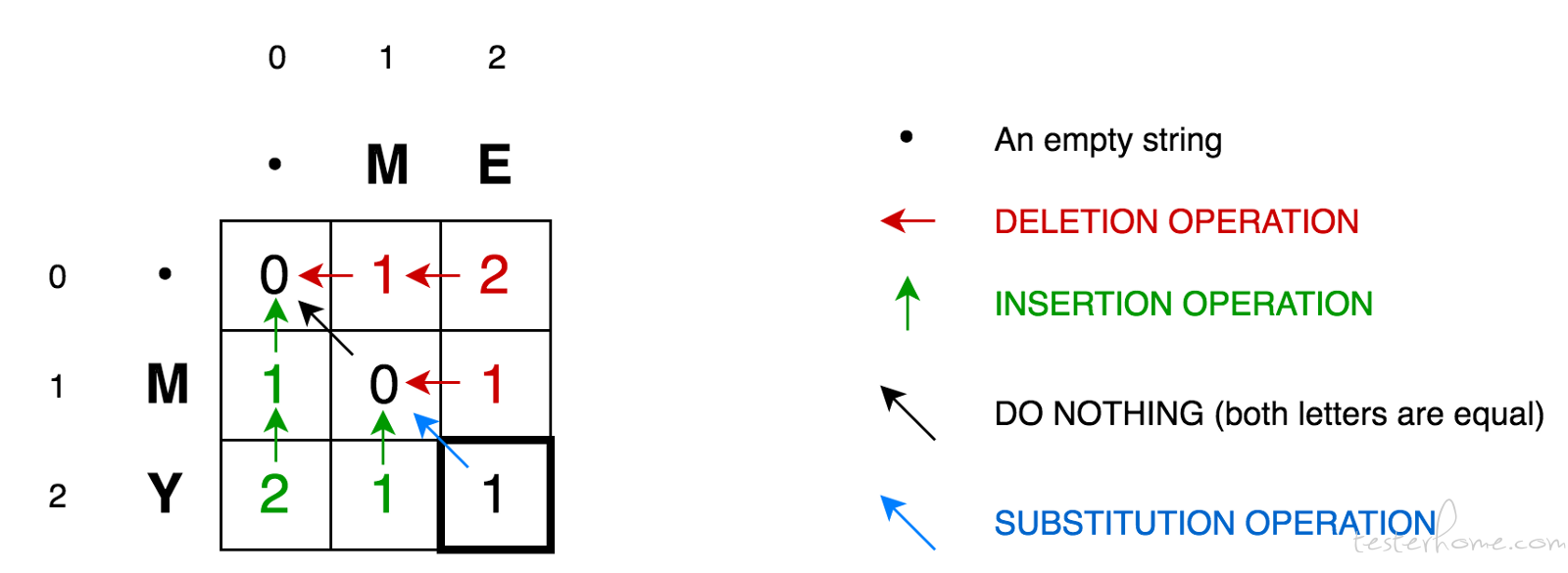
无序

精准匹配

对于无序的精准匹配，我们就采用了暴力法

精准匹配的 pseudo code

pairs = []
matched = {}

for li in range(len(left)):
    for ri in range(len(right)):
        if ri in matched:
            continue
        same = diff(left[li], right[ri])
        if same:
            pairs.append([left[li], right[ri]])
            matched[ri] = True
            break

就是两两的去比较，如果达到了「相等」的规则，那么就把他们匹配成一对。

模糊匹配

这边的「模糊匹配」和「有序 - 模糊匹配」是不一样的。一来是不需要再切割成多个区间了（无序！），二来编辑距离的算法也不再有效（还是因为无序，e.g. [a,b,c] 和 [c,b,a] 是完全一样的）

那这一块是比较有趣的部分，找了不少资料以后，觉得这个很适合匈牙利算法,下面是从 wiki 上摘录的匈牙利算法应用场景的例子：

你有三个工人：吉姆，史提夫和艾伦。 你需要其中一个清洁浴室，另一个打扫地板，第三个洗窗，但他们每个人对各项任务要求不同数目数量的钱。 以最低成本的分配工作的方式是什么？ 可以用工人做工的成本矩阵来表示该问题。例如：

	清洁浴室	打扫地板	洗窗
吉姆	$2	$3	$3
史提夫	$3	$2	$3
艾伦	$3	$3	$2

当把匈牙利方法应用于上面的表格时，会给出最低成本：为 6 美元，让吉姆清洁浴室、史提夫打扫地板、艾伦清洗窗户就可以达到这一结果。

套在我们的场景下，我们也会有这样的一个矩阵（参考上面的这张图）,那我们就是需要找到一份匹配的组合，使得总的相似度最大。

实现

这边整理了一下在实现的过程中碰到的过程和问题的记录。

递归

对于 json 的 diff 有一个绕不过去的就是递归。

在实际的过程中，还有一些问题需要解决。首先是，我们设计的 diff 逻辑必须采用递归,：以下面的为例子来看

# 基准
left = {
    "id": 1,
    "random": 12345，
    "set": [
        {"id":1, "set": [1,2,3]},
        {"id":2, "set": [4,5,6]}
    ]
}
#################################
# 对比
right = {
    "id": 3,
    "random": 6784，
    "set": [
        {"id":2, "set": [6,4,5]},
        {"id":1, "set": [3,1,2]},
    ]
}

上例中的left和right是否一致呢？

根据我们的「set 字段就代表无序」的规则，left和right是一致的，他们是没差的。实际上就是「set」字段的是否相等以来的是「left->set和right->set是否有差」=>「left->set->[\d+]->set和right->set->[\d+]->set是否有差」。

分数

这个一个对于所有的 diff 操作的抽象,所有的 diff 函数会返回一个 0~1 的浮点数来描述两个对象是否一样。
并且，在此基础上，我们可以算更复杂的相似度：

• 两个 object 的相似度就是所有的 key-value 对的相似度的和
• 两个 array 的相似度就是匹配完元素以后的相似度的和

如何报告 diff

由于递归的原因，报告的阶段应该选择在叶子结点。

区分「报告阶段」和「比较阶段」

为什么需要区分呢？因为在「匹配阶段」或者「递归比较阶段」的行为和「最终 diff 并且回报阶段」的行为很可能是不一样的：例如，以下面的 json 为例：

# 基准
left = [
    {
        "id": 1,
        "label": "label-1"，
    },
    {
        "id": 2,
        "label": "label-2"，
    }
]
#################################
# 对比
right = [
    {
        "id": 0,
        "label": "label-0"，
    },
    {
        "id": 1,
        "label": "label-1111"，
    },
    {
        "id": 2,
        "label": "label-2222"，
    }
]

如果业务上，我们的匹配条件是id相同，那么在「匹配阶段」，我们比较到id是否相同就达到目的了（以决定是否精准匹配），不需要再比较其他字段（也不能再比较），而真正汇报结果的时候，我们需要真正的比较其他字段（i.e. 汇报「label 的 diff」）。

因此加上了「drill」这个参数来判定是在哪一个阶段，避免需要定义多个算子。

用户自定义「相似」

何为「相似」？其实很难说，在不同的语境之下会有很大不同，例如

# 基准
left = [
    {
        "x": 92134,
        "y": 42351
    }
]
#################################
# 对比
right = [
    {
        "x": 91111,
        "y": 43333
    }
]

以上面为例，left->[0]和right->[0]是否「相似呢」？如果我们把他们解释成「某个用户的账户的可提现余额」那可能我们就说他们「有差」，并且说一个严重的 bug！而如果我们说他们是「平面坐标上两个点的坐标」，那也许我们要计算他们的欧式距离才能判断他们「有差/没差」。

因此很明显，所谓的「有差/没差」其实是跟业务、实际场景的关联度非常高的。因此为什么「json 工具难用」的原因在此：他太依赖场景了。

为了解决这个问题，我们必须提供「用户自定义两个元素的相似度/距离的方法」。

我们提供了BaseOperator供用户继承并实现diff这个方法。

下面展示了一个定义自定义算子的方法

def test_operator_custom():
    class L2DistanceOperator(BaseOperator):
        __operator_name__ = "operator:l2distance"
        __event__ = "operator:l2distance"

        def __init__(self, path_regex, distance_threshold):
            super().__init__(path_regex=path_regex)
            self.distance_threshold = distance_threshold

        def diff(self, level: 'TreeLevel', instance, drill: bool) -> Tuple[bool, float]:
            print("damn")
            distance = math.sqrt(
                (level.left["x"] - level.right["x"]) ** 2 + (level.left["y"] - level.right["y"]) ** 2
            )
            info = {
                "distance": distance,
                "distance_threshold": self.distance_threshold,
                "pass": distance < self.distance_threshold
            }

            if not drill:
                instance.report(self.__event__, level, info)
            return True, 1 if info["pass"] else 0

    left = {
        "distance_ok": {
            "x": 1,
            "y": 1
        },
        "distance_too_far": {
            "x": 5,
            "y": 5
        },
    }

    right = {
        "distance_ok": {
            "x": 2,
            "y": 2
        },
        "distance_too_far": {
            "x": 7,
            "y": 9
        },
    }

    ycm = YouchamaJsonDiffer(left, right, custom_operators=[
        L2DistanceOperator(f"distance.*", 3),
    ])


    equal = cm.diff()
    print("equal:", equal)
    print(ycm.to_dict(no_pairs=True))

结果如下

equal: False

{
    'operator:l2distance': [
        {
            'left': {'x': 1, 'y': 1}, 
            'right': {'x': 2, 'y': 2}, 
            'left_path': 'distance_ok',
             'right_path': 'distance_ok',
             'distance': 1.4142135623730951, 
             'distance_threshold': 3, 
             'pass': True
         },
        {
            'left': {'x': 5, 'y': 5}, 
            'right': {'x': 7, 'y': 9}, 
            'left_path': 'distance_too_far',
            'right_path': 'distance_too_far', 
            'distance': 4.47213595499958, 
            'distance_threshold': 3, 
            'pass': False
        }
    ]
}

注: 这边把所有匹配到的结果都记录了下来，并且用「pass」字段去区分是否通过规则，这部分用户自己决定就好。核心的是否有 diff 是diff返回的第二个float(这是一个 0~1 的浮点数，1 是一样，0 是不一样，中间地带在「相似度匹配」的时候用到)

优化与缓存

最后是优化的问题：由于上面说的递归、不同阶段、比较等等情况，会存在同一对元素被比较多次的情况，因此可以做一些优化来提升效率，现在的优化方案是「TreeLevel 的 hash+drill」为 key 来缓存结果。