
本篇我们讲红黑树的经典实现,Java 中对红黑树的实现便采用的是经典红黑树。前一篇文章我们介绍过左倾红黑树,它相对来说比较简单,需要大家看完上篇再来看这一篇,因为旋转等基础知识不会再本篇文章中赘述。本篇的大部分内容参考《算法导论》和 Java 实现红黑树的源码,希望大家能够有耐心的看完。
在正文开始之前我们先看如下问题:
关于红黑树和 AVL 树,大家可能看过 “在最坏情况下,AVL 树和红黑树的查找次数都是对数级别的,虽然红黑树的系数更高一些,但是没有本质的区别,是可以容忍的。AVL 树最致命的地方在于删除节点时旋转次数是对数级别的,而红黑树最多只需要 3 次旋转,这导致了红黑树应用相比于 AVL 树要广泛得多” 的观点,但实际上这并不是根本原因,根本原因是在以任意序列插入和删除操作混合进行的情况下,红黑树均摊时间复杂度保持在 O(1),而 AVL 树的均摊时间复杂度为 O(logn)。
经典红黑树与 2-3-4 搜索树同构,它相比于左倾红黑树(2-3 树)的实现,在维持红黑树平衡性开销更小。下文中我们会将经典红黑树简称为红黑树,开始吧:
2-3-4 搜索树是在 2-3 搜索树中增加了 4-节点,在前文中已经介绍过 4-节点,我们先来看一下 2-3-4 搜索树的样子:

新节点插入 2-节点或 3-节点的情况我们就不在这里赘述了,我们重点看一下新节点插入 4-节点的情况。当有新节点插入的节点为 4-节点时,需要先将 4-节点转换成 3 个 2-节点,再在其中的 2-节点中执行插入操作,如下所示,其中黄色节点为新插入的节点,对应了插入 4-节点中的四种情况:
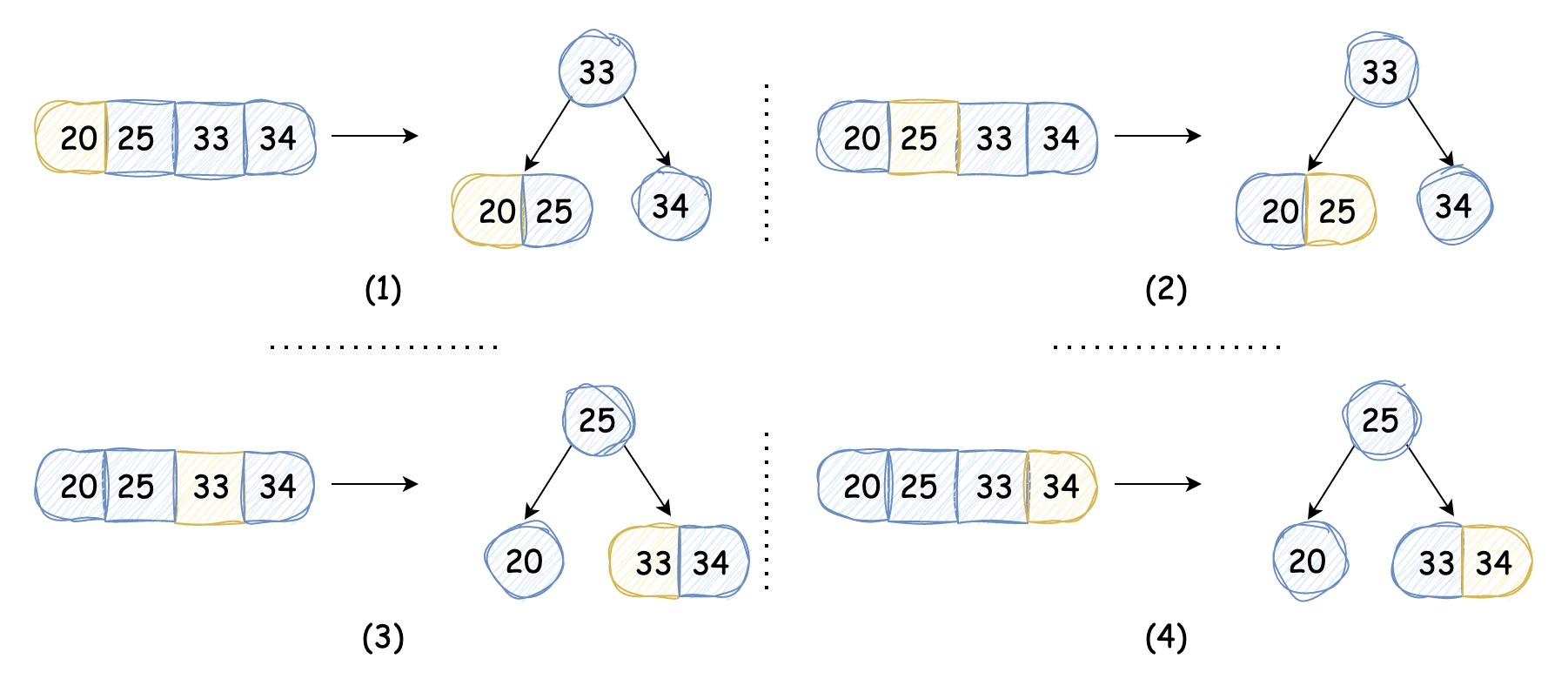
我们再以情况(4)为例,在 2-3-4 搜索树中执行插入值为 34 的节点:
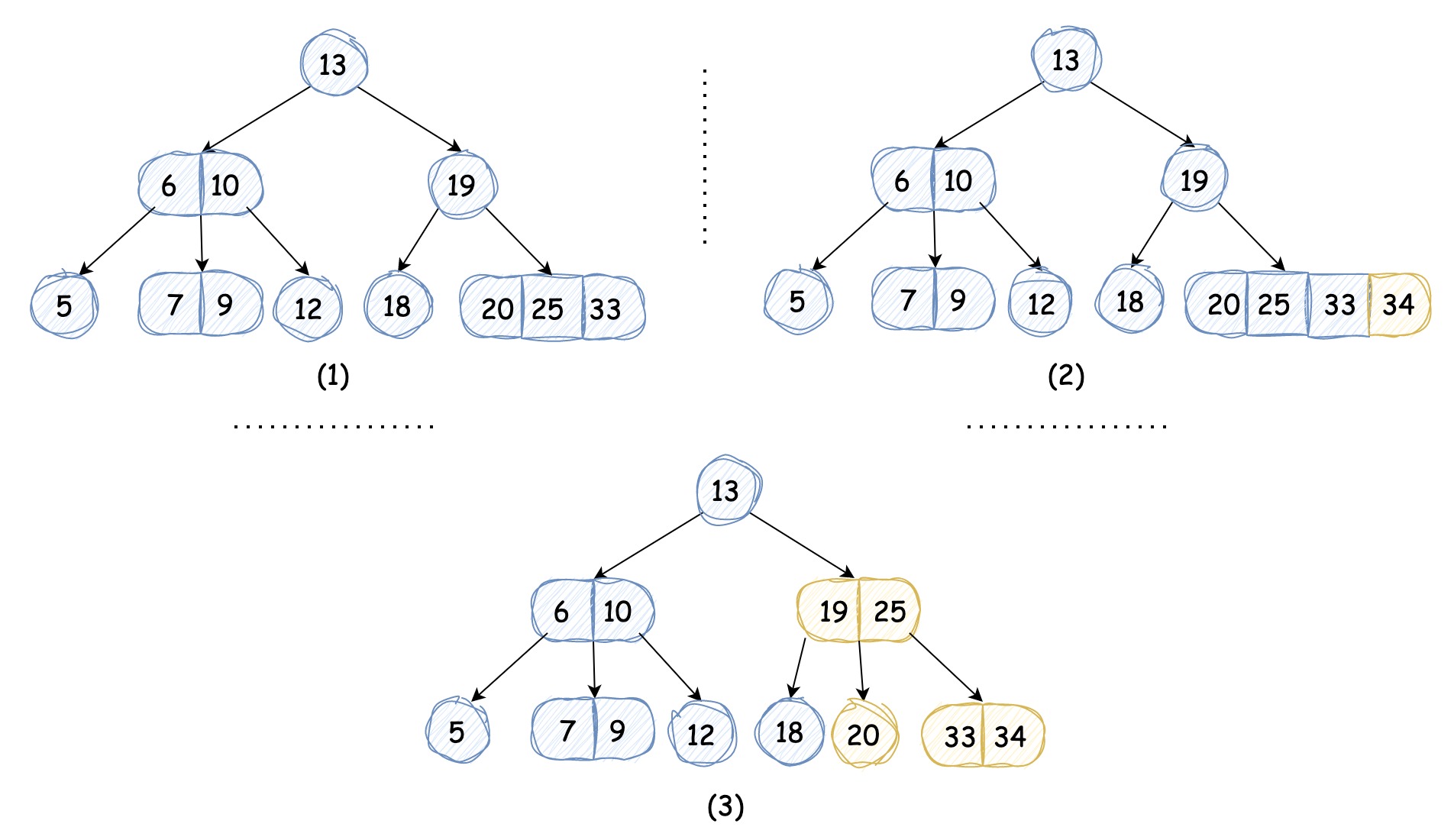
将 4-节点转换成 3 个 2-节点并完成插入新节点 34 后,需要将 “根节点 25” 插入到父节点中,如上图所示。这和我们在前文中在 2-3 搜索树中讲到的基本类似,需要不断分解临时的 5-节点,并将原来 4-节点分解成 3 个 2-节点的根节点插入到更高的父节点中,直到遇到 2-节点或 3-节点,将其转换成不需要继续分解的节点,如果最终插入到根节点后使其为 5-节点,同样需要进行分解再插入的操作,完成后树高加一。
2-3-4 树的插入操作使树本身的改变也是局部的,除了相关的节点和引用之外,不必修改和检查树的其他部分,这些局部变换不会影响到树的全局有序性和平衡性,在插入的过程中,2-3-4 树始终是完美平衡二叉树。
经典红黑树与 2-3-4 搜索树同构,如果我们把 2-3-4 搜索树样例转换成红黑树的话,会如下图所示(指向红色节点的链接我们同样也染成红色):
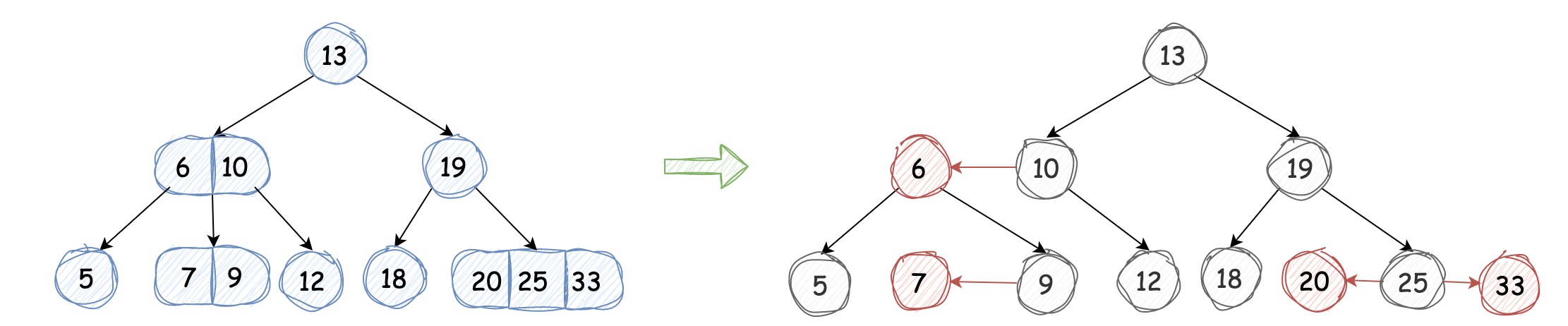
它满足如下性质:
节点颜色为红色或黑色
根节点是黑色的
叶子节点(null 节点)为黑色(null 节点在图中未画出来)
红色节点的两个子节点为黑色(不能出现连续的红色节点)
任意叶子节点到根节点路径上的黑色节点数量相同,即该树是黑色平衡的
黑色平衡这条性质我们在讲解左倾红黑树时已经讲过,在这里我们
不厌其烦地再叙述一遍:2-3-4 树始终能保持完美平衡,那么任意叶子节点到达根节点的距离是相等的,红黑树又是一颗2-3-4 搜索树,其中的黑链接是 2-3-4 搜索树中的普通链接,那么红黑树中被黑色链接引用的黑色节点也必然是完美平衡的,所以任意叶子节点到根节点路径上的黑色节点数量必然相同。
下面我们结合图示和 Java 中TreeMap源码来讲解红黑树的插入和删除节点操作:
static final class Entry<K,V> implements Map.Entry<K,V> {
K key;
V value;
Entry<K,V> left;
Entry<K,V> right;
Entry<K,V> parent;
boolean color = BLACK;
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
// ...
}
我们可以发现节点定义除了有表示颜色信息和左右子节点的引用外,还增加了parent针对父节点的引用。
插入 2-节点
直接将节点插入 2-节点的情况非常简单,如下图所示的两种情况,2-节点转换成 3-节点:
插入 3-节点
插入 3-节点我们需要分左斜 3-节点和右斜 3-节点两种情况讨论:
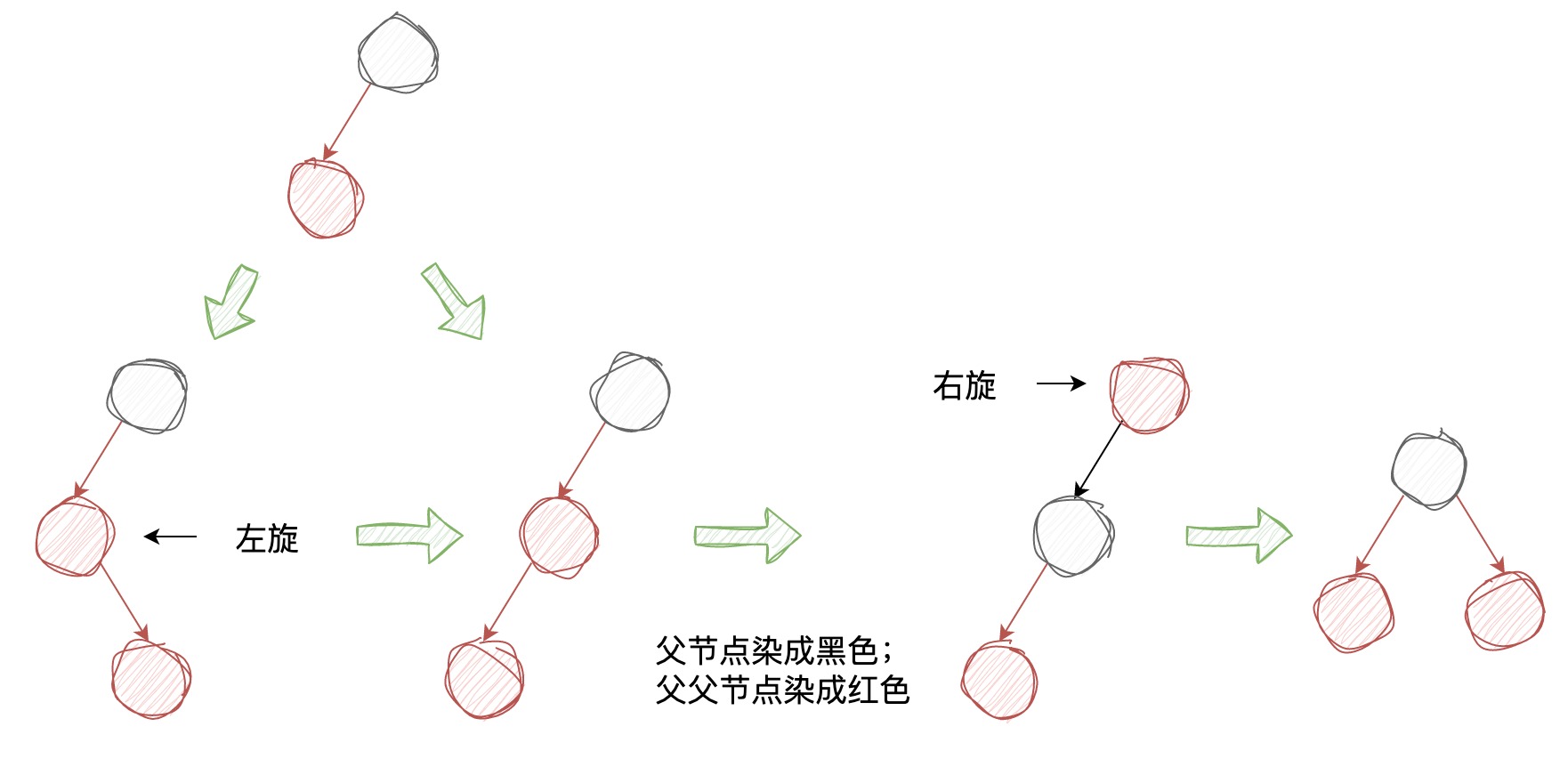
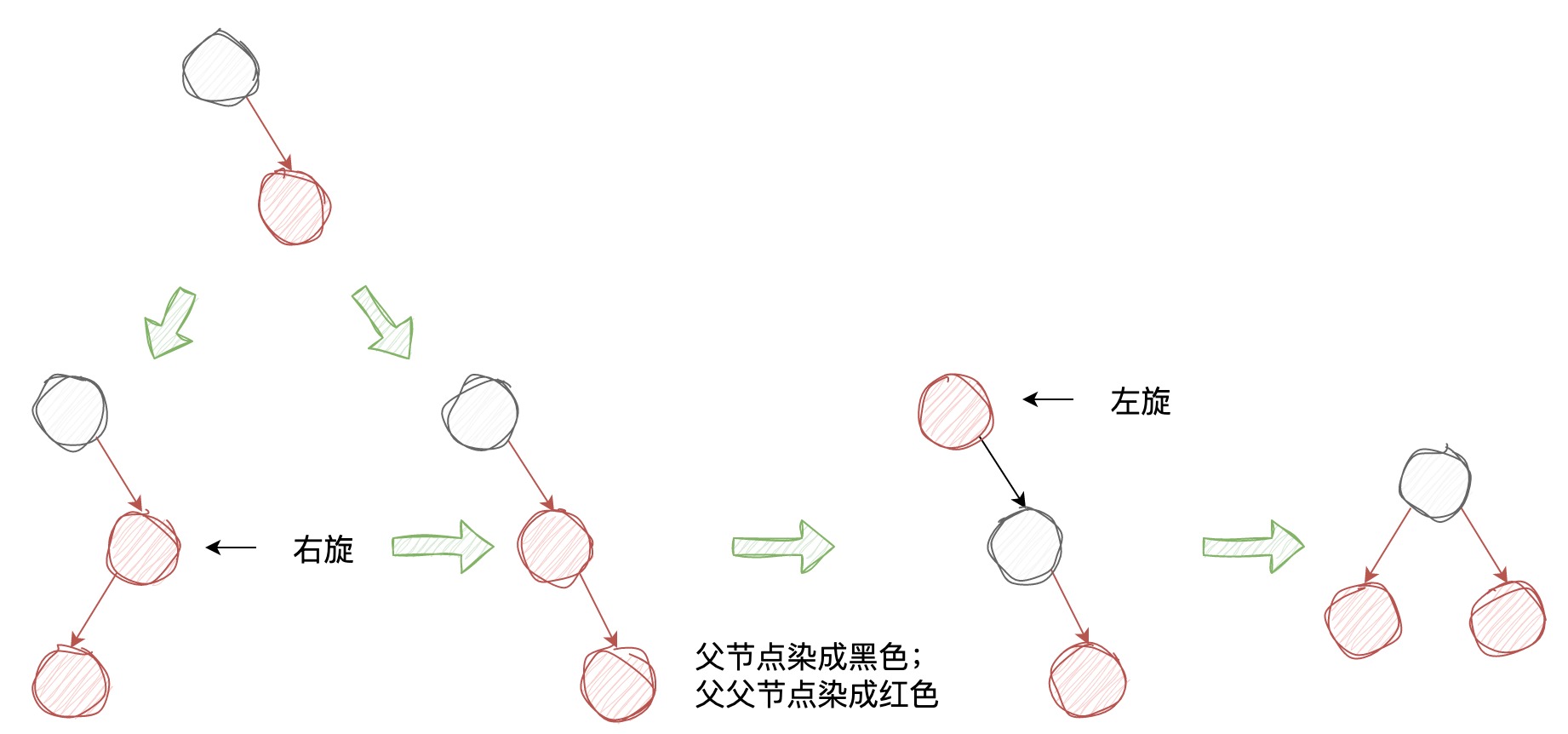
插入 4-节点
以上两种情况都是不会发生 “向上合并”,如果插入的 4-节点,需要将其分解成 3 个 2-节点,之后将 2-节点的 “根节点” 合并到它的父节点中(如果有的话),我们同样需要分情况讨论:
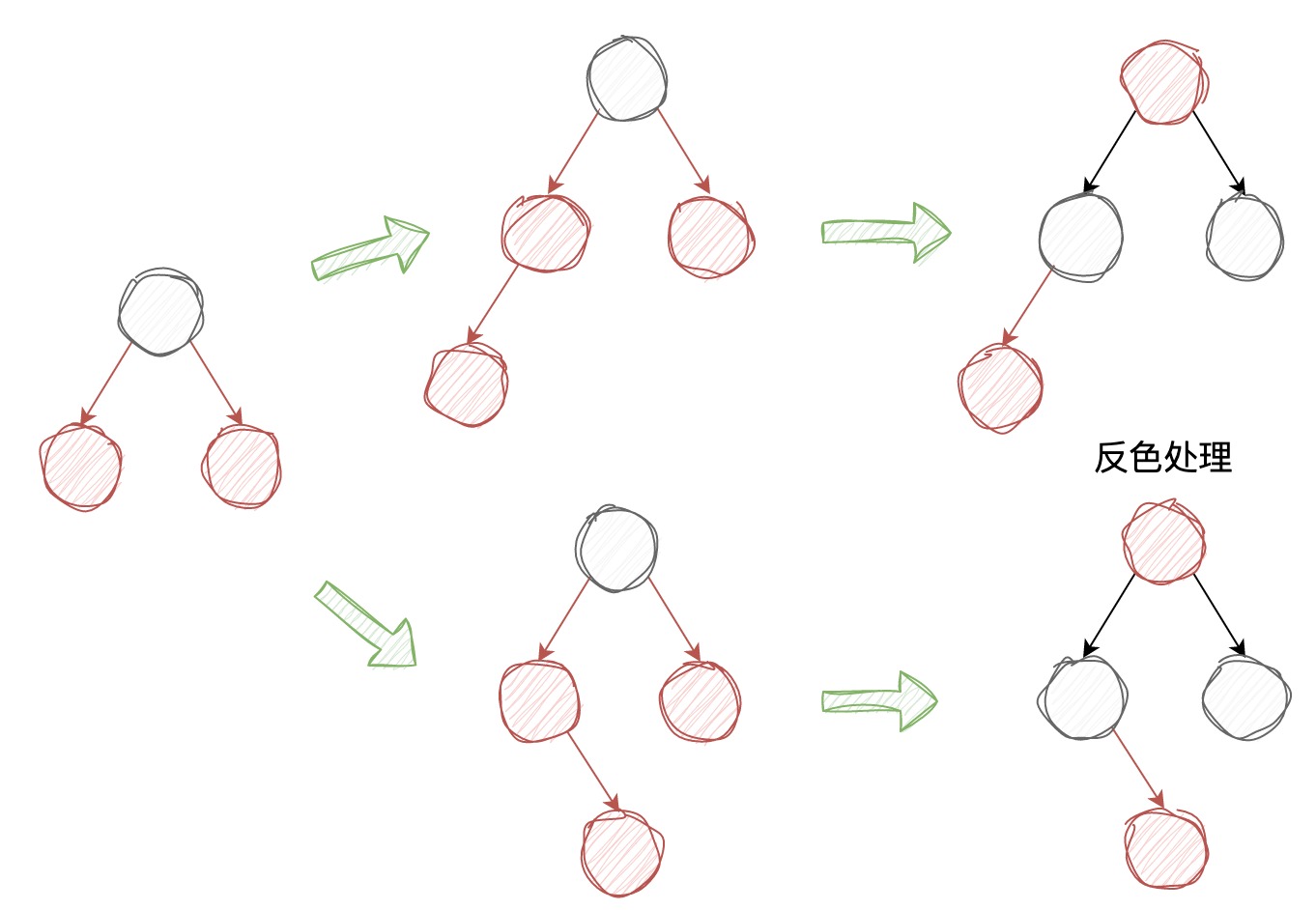
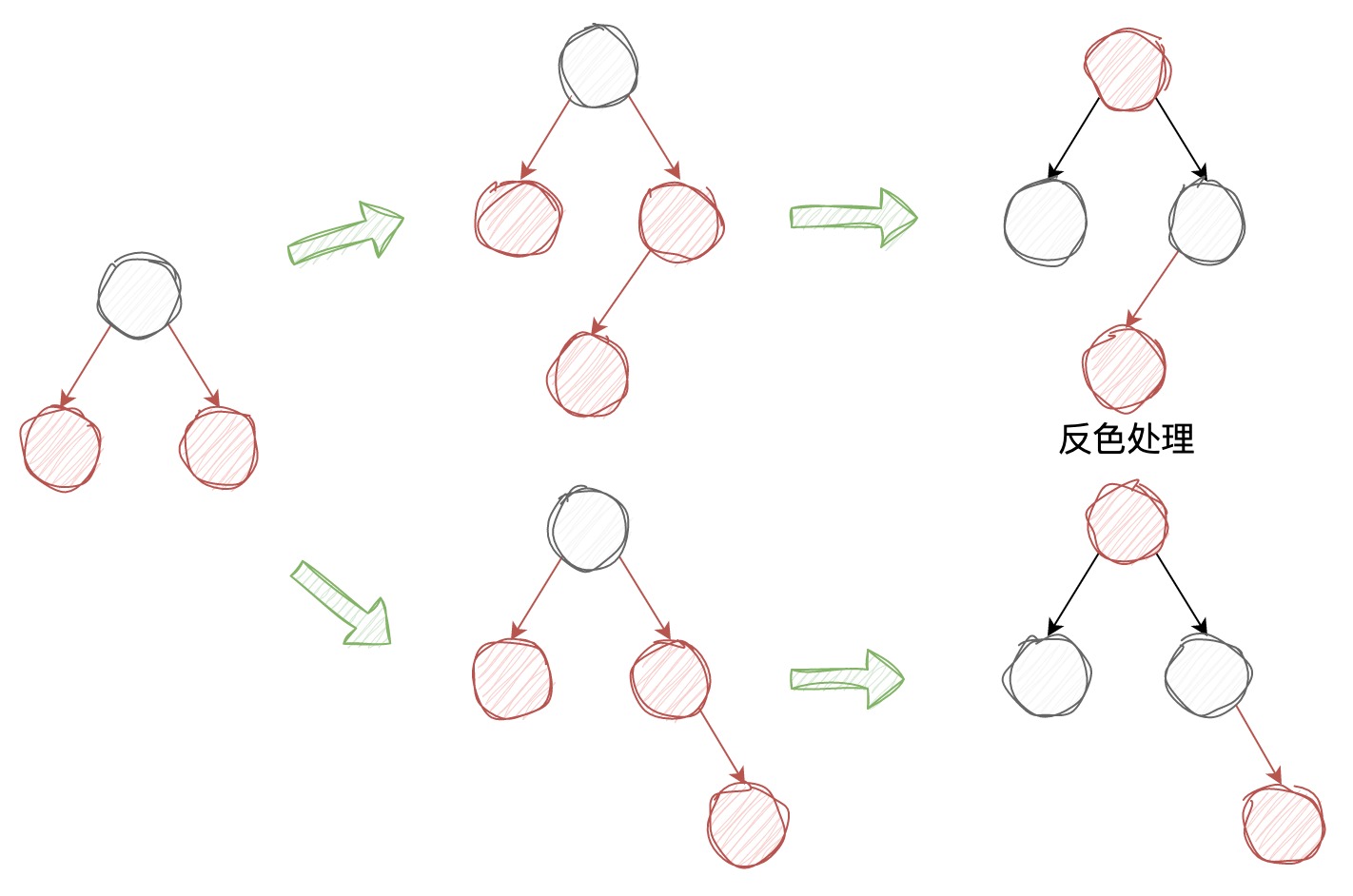
目前插入新节点的所有情况已经讨论完了,下面我们看一下TreeMap中的源码,大家注意其中的注释即可:
public V put(K key, V value) {
Entry<K,V> t = root;
// 插入第一个节点
if (t == null) {
compare(key, key);
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// 根据比较器找到插入节点的位置
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
// 根据大小关系添加新的节点
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
// *插入之后修复平衡操作*
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
需要重点关注fixAfterInsertion方法:
private void fixAfterInsertion(Entry<K,V> x) {
// 新插入的节点指定为红色
x.color = RED;
// 如果非空非根节点且有连续的红色节点出现,需要不断地修复平衡
while (x != null && x != root && x.parent.color == RED) {
// 插入节点后,出现连续红色的节点的位置在左侧
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 插入的是4-节点,对应插入4-节点的情况1
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
// 反色处理
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
// 处理父节点的父节点(因为该节点为红色,可能会发生向上合并的操作)
x = parentOf(parentOf(x));
} else {
// 如下步骤对应插入3-节点的情况1
// 插入的是3-节点的右节点
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
// 左旋父节点
rotateLeft(x);
}
// 现在转换成了插入位置为3-节点的左节点,父节点染成黑色
setColor(parentOf(x), BLACK);
// 父节点的父节点为红色
setColor(parentOf(parentOf(x)), RED);
// 右旋父节点的父节点,转换成4-节点
rotateRight(parentOf(parentOf(x)));
}
} else {
// 插入节点后,出现连续红色的节点的位置在右侧
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
// 插入的是4-节点,对应插入4-节点的情况2
if (colorOf(y) == RED) {
// 反色处理
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
// 处理父节点的父节点(因为该节点为红色,可能会发生向上合并的操作)
x = parentOf(parentOf(x));
} else {
// 如下步骤对应插入3-节点的情况2
// 插入的是3-节点的左节点
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
// 右旋父节点
rotateRight(x);
}
// 转换成了插入位置为3-节点的右节点,父节点为黑色
setColor(parentOf(x), BLACK);
// 父节点的父节点为红色
setColor(parentOf(parentOf(x)), RED);
// 左旋父节点的父节点,转换成4-节点
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 根节点始终为黑色
root.color = BLACK;
}
删除节点是红黑树中最复杂的实现,如果删除的是 3-节点或 4-节点(删除的是红色节点),那么移除该节点不会影响红黑树的平衡;如果删除的是 2-节点,需要在删除节点后向上修复红黑树的平衡,这也是其中最复杂的部分,下面我们按照《算法导论》中讨论的情况来分析,理解删除过程一定要对红黑树的性质非常熟悉(尤其是性质 5:红黑树始终都是黑色平衡的),书中将 2-节点移除后分了四种情况来讨论,记红黑树再平衡开始的节点为 x(x 节点为某 2-节点被移除后,拼接到该位置的节点),其兄弟节点为 w,如下:
情况 1:x 的兄弟节点 w 是红色的
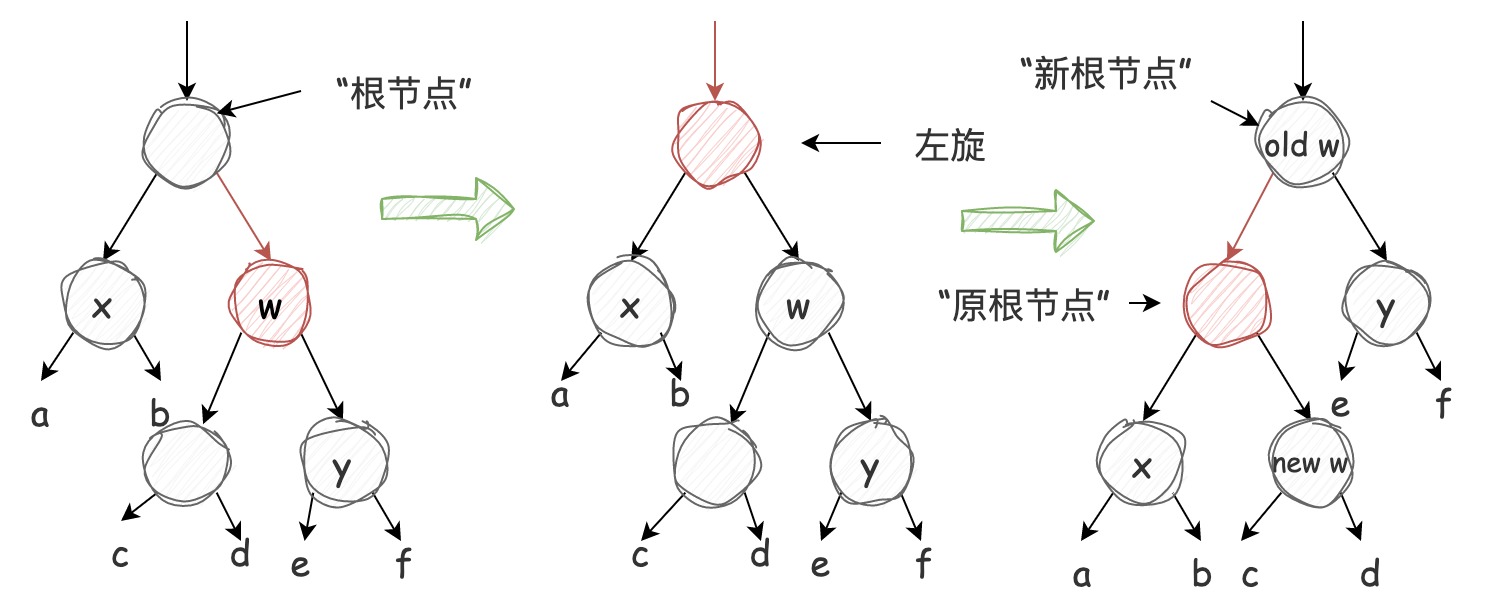
上图所示的局部红黑树在节点被移除前是黑色平衡的,那么从根节点到 a 子树的黑色节点数量应为 3。当节点被移除后,根节点到 a 子树的黑色节点数量为 2(如图上所示);根节点到 c 子树路径上的黑色节点数量为 2。
经过反色和左旋处理后,原根节点被染红,现在从 “新根节点” 到 a 子树的黑色节点数量仍然为 2,没有新增到 3,所以还是黑色不平衡;到 c 子树路径上的黑色节点数量为 2,与操作前一致,没有影响到红黑树的性质。
情况 1 在反色和左旋后会变成情况 2、情况 3 或情况 4 继续处理,这其实不难理解,结合红黑树的性质 5,反色和左旋操作使根节点到某子树路径上的黑色节点数量并没有改变,而我们执行删除操作时已经将该路径上移除一个黑色节点了,所以 “根节点” 到某子树的路径上依然需要补充一个黑色节点才能满足黑色平衡,关键思想在于:从根节点到每棵子树路径上黑色节点的数量不能被改变,性质 5 在删除节点和变换前后都需要成立。
情况 2:x 的兄弟节点 w 是黑色的,而且 w 的两个子节点都是黑色的
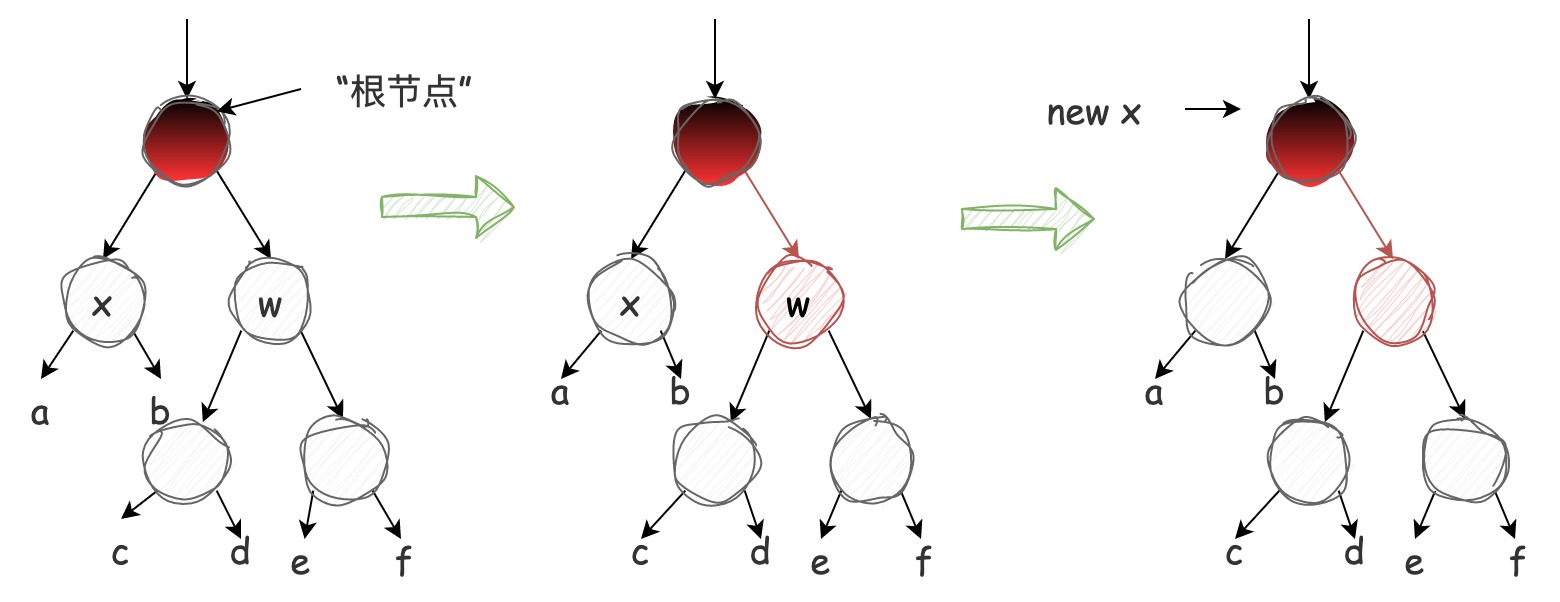
注意图中的红黑渐变色表示该节点可能是黑色节点也可能是红色节点。在该情况下,兄弟节点的两个子节点都是黑色的,在某节点被删除前从根节点到 a 子树和 c 子树路径上的根节点数量都是 2(忽略不确定颜色的根节点)。删除节点后根节点到 a 子树路径上的黑色节点数量为 1,如果我们将 w 节点染红,那么根节点到 c 子树路径上的黑色节点数量减少为 1,那么从根节点到图示中所有子树路径上黑色节点数量都一致了,也就是说图示中的局部红黑树满足黑色平衡的条件了。此时需要将 x 指向它的父节点再重复(while)修复的过程。
情况 3:x 的兄弟节点 w 是黑色的,w 的左节点是红色的,w 的右节点是黑色的
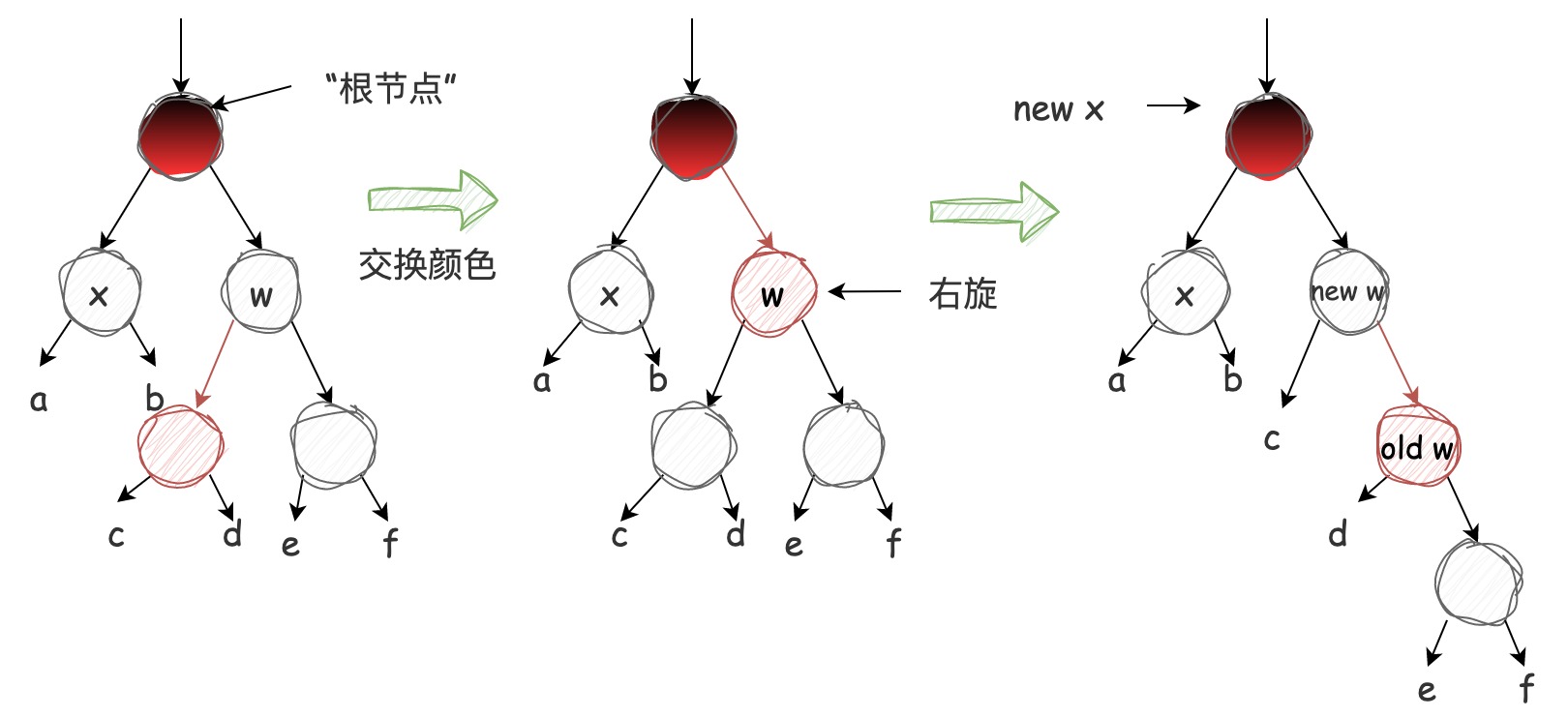
这种情况下,根节点到子树 e 路径上黑色节点数量为 2,经过交换 w 和 w.left 的颜色和右旋操作后并不影响红黑树的性质,这样就将情况 3 转换成了情况 4。
情况 4:x 的兄弟节点 w 是黑色的,且 w 的右节点是红色的

在情况 4 下,根节点到 a 子树路径上的黑色节点数量为 1,想达到黑色平衡需要增加到 2。通过交换 w 节点和 x.parent 节点的颜色,再将 w.right 节点染黑,之后对 x.parent 节点执行左旋操作后,使得根节点到到 a 子树路径上的黑色节点增加到了 2,并且到达其他 c, d, e, f 子树路径上的黑色节点数量不变,不破坏红黑树的性质,操作完毕后将 x 指向根节点,结束循环,因为此时红黑树满足所有性质。
现在我们已经分析完了删除 2-节点后的四种不同情况,都需要通过染色和旋转操作让红黑树再次黑色平衡,下面我们看下TreeMap中remove方法的实现,需要关注其中的注释信息:
/**
* 删除节点
*/
public V remove(Object key) {
// 找到要删除的节点
Entry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
// 执行删除操作
deleteEntry(p);
return oldValue;
}
接下来我们看一下删除操作的执行逻辑:
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// 如果该节点有左右子节点,则它是一个要被删除的内部节点
// 那么需要找到该节点的“后继节点”,找到之后删除任务则变为了删除该后继节点
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
// 执行完上述代码块后,被删除节点要么为叶子节点,要么为只有左子树或右子树的节点
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
// 被删除节点有左子树或右子树
if (replacement != null) {
// 修正节点的父节点引用关系
replacement.parent = p.parent;
// 被删除节点为根节点的关系
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
// 被删除的节点是左节点
p.parent.left = replacement;
else
// 被删除的节点是右节点
p.parent.right = replacement;
// 断开被删除节点的所有引用关系
p.left = p.right = p.parent = null;
// 如果被删除节点为2-节点,需要执行再平衡操作
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) {
// 红黑树只有一个节点的情况
root = null;
} else {
// 删除叶子节点,如果该节点为2-节点那么需要再平衡修复
if (p.color == BLACK)
fixAfterDeletion(p);
// 断开引用关系
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
// 获取 t 节点的后继节点
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) {
// 右子树不为空,则右子树中最小的节点为该节点的后继节点
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else {
// ...
}
}
fixAfterDeletion为删除后再平衡方法,需要大家关注其中的注释信息:
private void fixAfterDeletion(Entry<K,V> x) {
// 非根节点和当前节点是黑色的才需要修复平衡
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
// 情况 1
if (colorOf(sib) == RED) {
// 反色处理:兄弟节点染黑,父节点染红
setColor(sib, BLACK);
setColor(parentOf(x), RED);
// 左旋父节点
rotateLeft(parentOf(x));
// 新的兄弟节点
sib = rightOf(parentOf(x));
}
// 情况 2
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
// 将兄弟节点染红后,x指向父节点引用,继续修复平衡
setColor(sib, RED);
x = parentOf(x);
} else {
// 情况 3
if (colorOf(rightOf(sib)) == BLACK) {
// 交换颜色:兄弟节点左节点染黑,兄弟节点染红
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
// 右旋兄弟节点
rotateRight(sib);
// 新的兄弟节点
sib = rightOf(parentOf(x));
}
// 情况 4
// 交换兄弟节点和父节点的颜色
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
// 将兄弟节点的右节点由红染黑
setColor(rightOf(sib), BLACK);
// 左旋父节点
rotateLeft(parentOf(x));
// 满足红黑树的性质,指向根节点循环结束
x = root;
}
} else {
// 以下是镜像操作
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
// 情况 2,x 为红色节点时跳出循环,需要将 x 节点染黑
// 因为红黑树中不存在连续的红色节点
setColor(x, BLACK);
}
红黑树执行删除方法的时间复杂度是多少呢?含有 n 个节点的红黑树的高度为 logn,不调用fixAfterDeletion方法时,复杂度为 O(logn),在fixAfterDeletion中,情况 1, 3, 4 在各执行常数次的颜色改变和至多 3 次旋转后便终止,只有在情况 2 中才可能重复修复平衡,指针也至多上升 O(logn) 次,且没有任何旋转操作,所以fixAfterDeletion复杂度为 O(logn),最多旋转 3 次,因此红黑树删除方法的时间复杂度为 O(logn)。
《算法导论》:第 13 章 红黑树
知乎 - 关于 AVL 树和红黑树的一点看法
LeetCode - 红黑树从入门到看开
博客园 - 红黑树的删除
作者:京东物流 王奕龙
来源:京东云开发者社区 自猿其说 Tech 转载请注明来源
