
作者:京东零售 路卫强
本篇的目的是从三个不均匀性的角度,对 AB 实验进行一个认知的普及,最终着重讲述 AB 实验的一个普遍的问题,即实验准确度问题。
在首页中,我们是用红色基调还是绿色基调,是采用门店小列表外 + 商品 feed(左图),还是采用门店大列表囊括商品 feed(右图),哪种更吸引用户浏览下单呢,简单来处理让 50% 的用户看到左图效果,让 50% 的用户看到右图效果,最终通过点击量,单量等指标进行比对得出结论,这是典型的 AB 实验场景


A/B 实验就是针对想迭代的产品功能,提供两种不同的备选解决方案,然后让一部分用户使用方案 A,另一部分用户使用方案 B,最终通过实验数据对比来确定最优方案。
从定义里我们就可以看出来,最直观的一个概念,就是用户的分流,此时就涉及到分流人数是否均匀的问题,即人数比例的均匀性。
目前 AB 实验的分流核心算法是通过的哈希算法,假设我们按用户名做为分流因子,使用 murmurhash 算法,以 100 桶制为例,确定一个人的位置的算法就是
//将用户名通过hash算法计算出一个整数
int hashNum = MurmurHash3.murmurhash3_x86_32(useName)
//整数值对100取模
int bucket = hashNum % 100;
当我们定义一个实验两个策略的人数均为 50% 时,那么
bucket 为 0-49 的用户由 AB 系统标记为 A,业务系统根据 A 标记,使得用户使用方案 A
bucket 为 50-99 的用户由 AB 系统标记为 B,业务系统根据 B 标记,使得用户使用方案 B。
可是我们都知道哈希算法并不是绝对均匀的,当 100 人时,基本上不会出现有 50 个人走 A,50 个人走 B,但是 1 万个人的时候,两部分流量可能就接近了 1:1,10 万人的时候可能更接近 1:1。
之前有位运营的同学问过,为什么不能用一种很均匀的算法,比如第一个人来了,放入 A,第二个人来了放入 B,第三个人来了放入 A,第四个人来了放入 B....,这样一天 1W 个人来,5000 个取 A 策略,5000 个取 B 策略。
假设我们真的这么做了,第一天是 OK 的,第二天进 A 只来了 4000 人,这样还是不均匀的,如果你第二天仍然按第一天的规则重新分配,这样会有一部分人乱了策略,不符合我们固定人群走固定策略的实验目的。
所以说这个不均匀是无解的,HASH 算法是目前最理想的解决方案,前提是你需要一定的流量,流量越大,分流相对就比较准确。
我们假设流量足够大,人数比例很均匀了,但是还有个问题就是人群素质的均匀问题。这里的素质包括消费能力,活跃度,年龄等各种人群因素。
假设现在我们的活动统一采用的 A 策略(现状),我们想验证一下 B 策略(新策略)会不会带来客单价的提升,就直接做了 AB 实验,还按 1:1 比例来分流,发现使用 A 方案的人群客单价是 100,使用客单价 B 的人群是 96,此时我们能认为原有 A 方案优于 B 方案吗?其实是不能的,怎样确定这种人群素质的差异呢,可以采用 AA 实验,就是两部分人都走 A,进行分开统计,可能会发现,位于 0-49 桶的人群本身客单价就是 100,而位于 50-99 桶的人群可能只有 94,这么看来 B 方案是能提升客单价的,因为位于 50-99 桶的人群本身指标就差一些。
当然 AA 不是必须的,可能你有整体的客单价指标,上了 B 策略后发现整体提升了,这种情况相当于灰度验证了,但实际情况是比较复杂的,整体指标你是不清楚的(因为这里的整体可能只是你取的业务中的一部分流量)。
所以解决素质不均匀的手段就是采用 AA 提前确定差异性,再在这个差异性基础上看差异的变化。
这个不均匀性是最复杂的,一般做实验我们走两种极端:
第一种是完全不复用人群,每个实验人群都是独立的,这样的话效果比较准确,但是弊端是,当所有流量都被用去后,不能有新实验开始,必须等待有结束的实验后才能继续做。
第二种,所有实验都用全部流量,此时我们认为实验虽然互相之间有影响,但是这种影响是正交的,量大的时候应该是均匀的,如下图所示,P 实验的两个策略人群,到 Q 实验时,对 Q 的两个策略影响是均匀的。
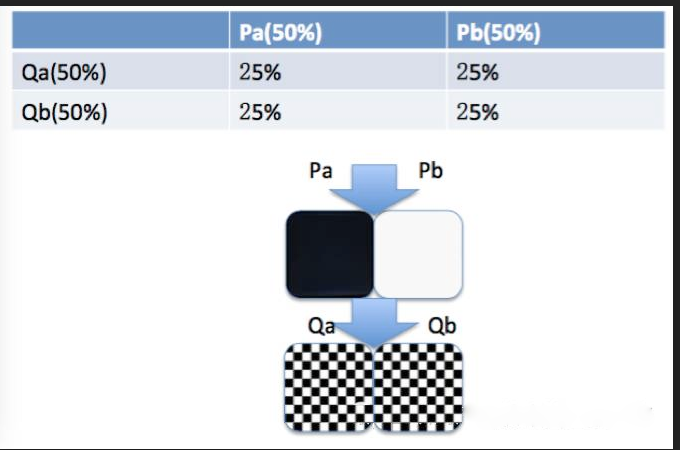
这种可以满足无限个实验,想做多少实验都可以,但弊端是,实验太多,必然有影响不均匀的,且我们无法消除这种不均匀。
所以我们想能不能结合以上两种情况来处理呢,结合 google 的 Overlapping Experiment Infrastructure 文章我们设计出分层的实验管理模型
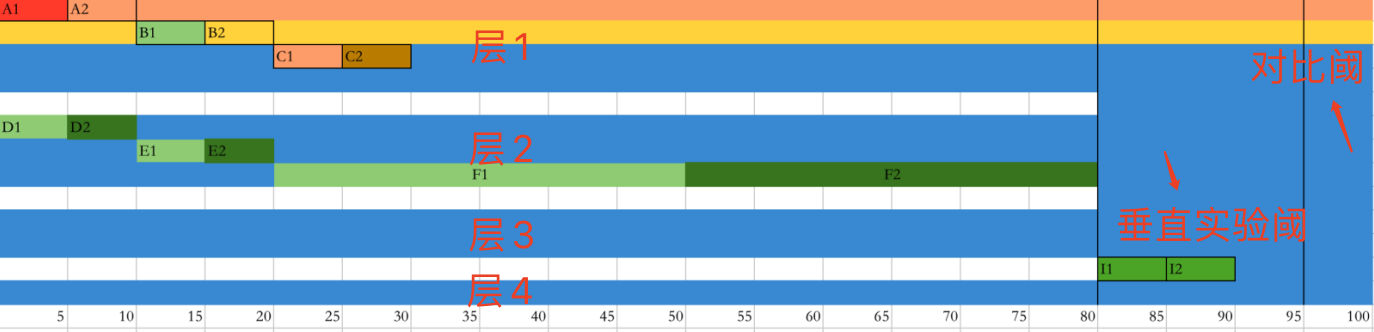
首先我们将总流量分成两部分,正交域,垂直域(含对比区)
我们假设如图取 80% 的流量用做正交阈,20% 用作垂直域,垂直域中有 5% 用做对比区。
上图正交域下 4 个层,层内实验流量互斥,层间实验流量正交,我们将可能会互相影响的实验放到同一层内进行流量互斥,而影响不大的实验可以放到不同层内。
垂直域中的实验流量只能互斥,且不与任何实验正交,可以理解用最纯正的流量做实验,可以 I1 和 I2 两个策略间对比,也可以 I1 或 I2 和对比域(现状)比对。
那此时有一个很重要的问题需要解决,我们怎么确定哪些实验互相影响较大,需要放到同一层下。
有一些简单标准,比如入口不一样,目标不一样等等,这种可以放到不同层,我们可以忽略正交不均匀的问题,反之就不行。
比如活动页劵对单量提升度的实验和会员页面入会效果的实验,就可以放到不同层。
而首页上满减活动实验对客单价提升的实验和同样首页买赠活动对客单价提升的实验,最好是不共用用户,放到同层比较合适。
但对于很多实验是不太容易通过简单规则来确定的,需要大数据的同学和产品,甚至研发来共同决定实验放到哪些层和哪些实验互斥,这确实在实际的运作中是最难的点。
总之采用这种策略,可以复用流量的同时还可以降低不必要的互相影响,比较综合考虑了流量和准确度问题。
现在我们对以上问题进行总结,从问题到解决方案上来认识 ab 实验
1、人群做不到绝对的均匀,只能通过 HASH 算法,结合一定的流量来解决。
2、通过 AA 实验,来提前确定人群素质的不均匀。最终的实验数据结合 AA 实验数据来确定最终效果。
3、设计出正交垂直域,正交阈内多个层,每个层内放可能相互影响的实验,层内互斥,层间正交,保留垂直域,为要求精准的实验留出流量,来解决实验间相互影响的问题。
本篇从核心分流与实验间相互影响角度讲解 ab 实验,希望能引起大家在做实验前能有更多的思考,来更准确的验证自己想要的效果,希望大家有兴趣的可以留言讨论。
