谁说算法在测试领域无用？ 我昨天就遇到了一个很恶心的技术问题：

这是一个汉字字符串： "银行卡测试"

我要求出他的拼音首字母组合，

预期："yhkcs"

实际："yhqcs"

没错，它含有一个多音字：卡

念 ka 或者 qia

我的需求就变成了：我要获取它所有可能的首字母组合，放到一个大列表中。

通过第三方 pinyin 库，我成功的拿到了他们首字母组成的二维数组，每个元素就是一个字的首字母列表：

"银行卡测试" = [['y'],['h'],['q','k'],['c'],['s']]

这个的最终结果应该是：

['yhqcs','yhkcs'] 长度为 2

当然，换一个多个多音字的：

"长卡测" = [['c','z'],['q','k'],['c']]

预期结果：

['cqc','ckc','zqc','zkc'] 长度为 4

最终元素总个数为每个子列表长度的乘积。

当然还有更复杂的：

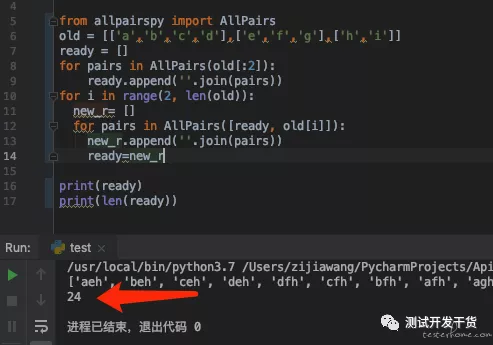
[['a','b','c','d'],['e','f','g'],['h','i']]

这个预期大列表的长度应该是 4*3*2 = 24

那么以上的需求用代码如何实现？

苦思冥想，写出了一套算法，我觉得我应该是唯一一个这么写的：

from allpairspy import AllPairs
old = [['a','b','c','d'],['e','f','g'],['h','i']]
ready = []
for pairs in AllPairs(old[:2]):
    ready.append(''.join(pairs))
for i in range(2, len(old)):
  new_r= []
  for pairs in AllPairs([ready, old[i]]):
    new_r.append(''.join(pairs))
    ready=new_r

print(ready)
print(len(ready))

一点问题没有。

至于为什么我会想出这个解决办法呢？

我给大家说一下思路，非常有意思

首先我觉得直接去写递归 很麻烦。效率也不行，就想着有没有野路子搞定。

然后突然想到，这一个一个的子列表，就好像是我们测试中面对一个功能界面

上的一个一个多选输入框，而子列表内不确定数量的字母，就像是这些多选框内的子选项。

我们平时遇到要测试这种功能的时候，要怎么做呢？目的就是要尽可能的测出所有组合情况！

即每个下拉多选框只能选一个。多个框的各种组合我都要测到。

他们之间很明显没有任何逻辑强关联，这时我们应该首选 黑盒用例设计方法中的 正交！

是的正交，它可以自动生成各种情况对应的组合，每种组合就是一条最终用例！

但是！

正交算法的出现 就是为了避免穷尽测试，而我这次的需求就是要穷尽所有可能组合。

所以正交算法要稍微改一改了，毕竟这个第三方算法性能很好，我利用上性能绝对错不了！

正交的基本原则是 保证多个输入条件中，任何一个的子状态，和任何另外一个输入中的子状态 都同时出现过 即可。最终正交算法出来的所有组合数量，肯定是远小于全部组合的。

比如：

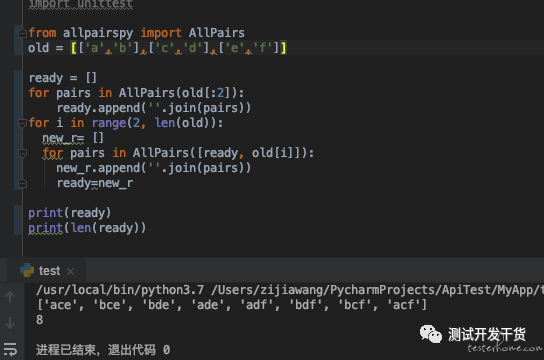
[['a','b'],['c','d'],['e','f']]

穷尽的数量应该是：2*2*2 = 8

而正交算法的数量：

['a', 'c', 'e']

['b', 'd', 'e']

['b', 'c', 'f']

['a', 'd', 'f']

最终 4 种，这 4 种你可以发现，任何俩个子列表的任何子元素都同时出现过。

比如：a 和 f ，有。

d 和 e 也有。

所以正交算法是为了降低我们测试用例数量，但又保证全面覆盖的东西。

但是这里我们要如何应用它以便让其变成输出穷尽所有的 8 种结果呢？

很简单，当只有俩个子列表，也就是只有俩个输入的时候。那么此时，正交算法的结果和穷尽结果 是完全相等的。

也就是说，我这个需求虽然可能有 4 个甚至更多个子列表，但是我只要用正交算法每次只算其中俩个子列表的穷尽，然后再把这个穷尽的结果当作一个新的子列表，再去和另一个新的子列表去计算穷尽，然后再把结果当作一个新的子列表再去和下一个子列表计算穷尽，直到没有子列表了，这时候的新的子列表就是最终结果！

大家是不是看到比较绕？

我用图来说明：

每次这样叠加算出后 最后就是最终结果。安全快捷准确！

然后就成了最上面的我分享的那个最终算法。

有兴趣的可以试试。当然我觉得 我应该是唯一一个靠 这么曲线救国的做法的测试了吧。

能想出这个方法，首先要感谢

我庞大精通的测试理论基础：黑盒测试用例设计方法 - 正交法

研究过正交的第三方 python 函数: allpairspy

长年刷 leetcode 练就的骚操作思维

所以小伙伴们，千万不要再说刷 leetcode，写算法对我们测试没有用了。