学习计划
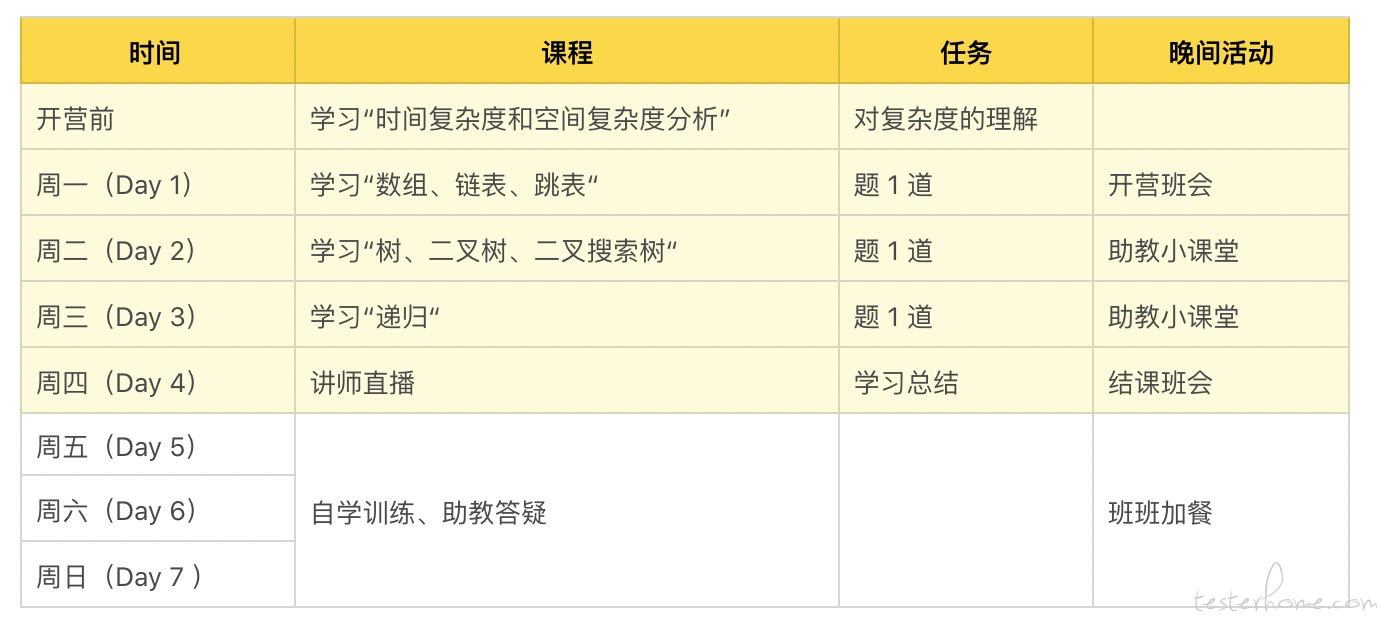
由于每天都需要写学习心得和作业,所以写此贴作为笔记。也希望可以帮助到有需要的同学。
全文内容主要源于极客大学的算法课,仅作为笔记使用。
学习计划
由于每天都需要写学习心得和作业,所以写此贴作为笔记。也希望可以帮助到有需要的同学。
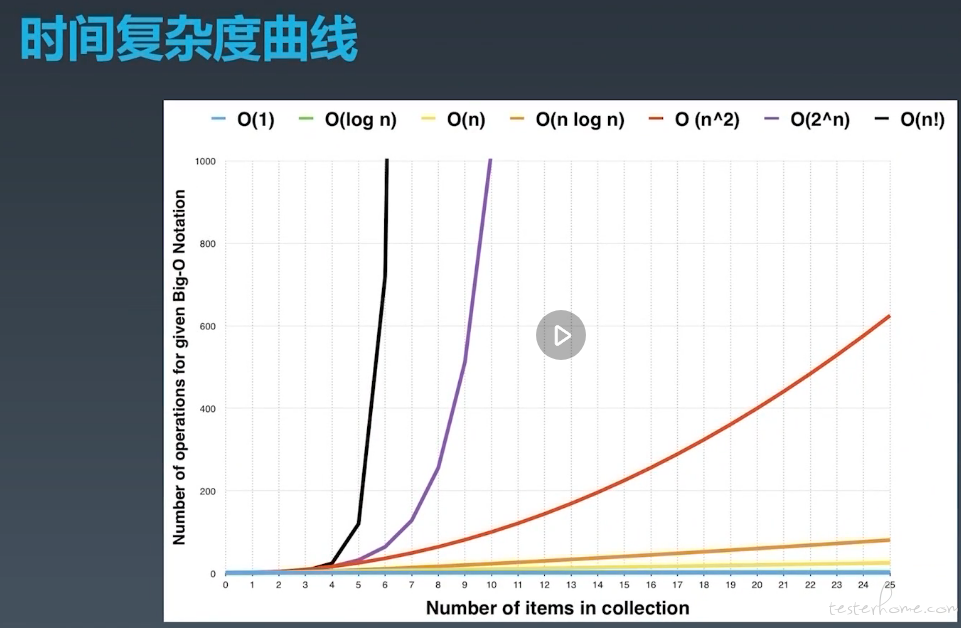
从图中可以看出,当 n 小于 5 时,不同的时间复杂度耗时差不多。
当 n 增大时,不同时间复杂度算法耗时差距非常大。所以也就不难理解,大型公司对算法的要求越来越高,是因为当遇到大数据量处理时,不同的算法能力,需要的服务器成本和代码性能是有天壤之别的。
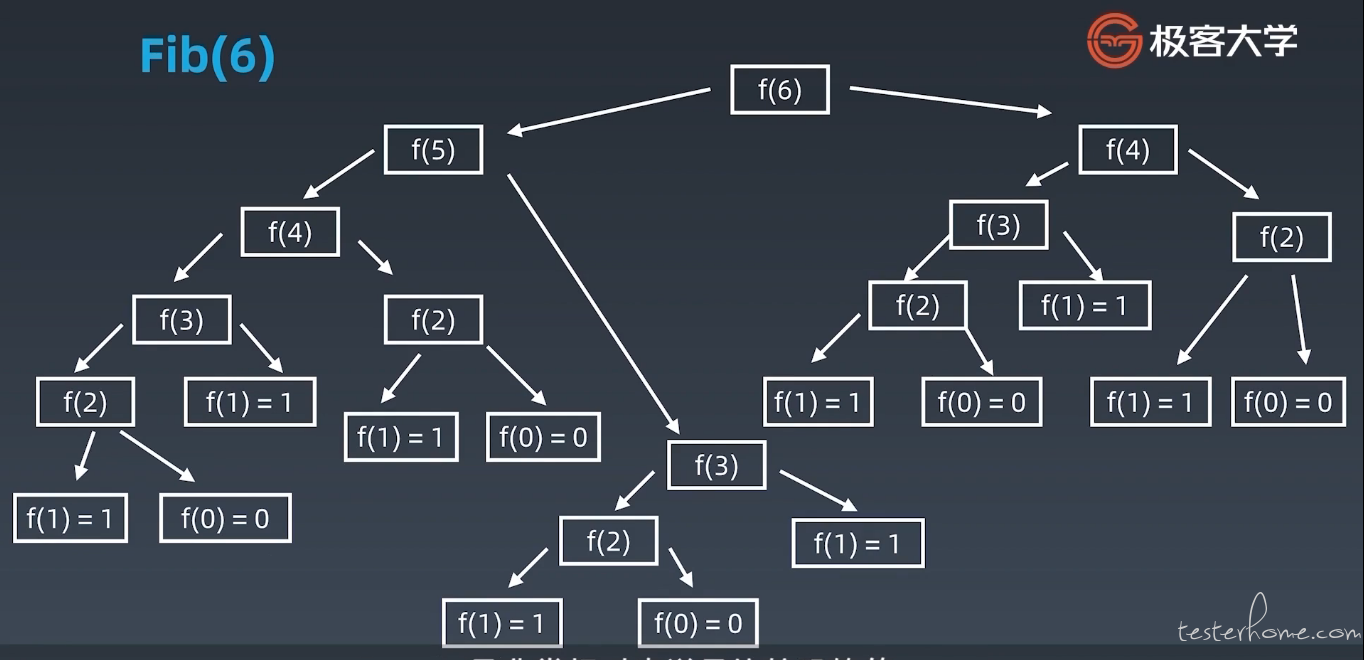
比如:斐波那契数列
Fib: 1, 1, 2, 3, 5, 8, 13, 21, 34...
方法定义:F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*)
def fib(n: int):
if n < 2: return n
return fib(n-1) + fib(n-2)
绘制递归图,以 n=6 为例:
常用算法应用主定理:(记住如下算法对应公式,并尝试理解)

空间复杂度和时间复杂度的情况类似,但是更加简单。
如果代码中开了数组,则数组的长度基本就是空间复杂度。
比如:
如果代码中有递归,那么递归最大深度,就是空间复杂度的最大值。如果递归里面又开了数组,那么两者中的最大值就是空间复杂度。
详见 leetcode 的爬楼梯示例:爬楼梯题解
时间复杂度:假设入参为 n,程序运行的次数与 n 的关系,即为时间复杂度。
时间复杂度优化顺序:O(1) > O(log n) > O(n) > O(n2) > O(n3) > O(2n) > O(n!)
空间复杂度:代码中数组的大小或递归深度的最大值。
空间复杂度优化顺序:O(1) > O(log n) > O(n) > O(n2) > O(n3) > O(2n) > O(n!)
为什么复杂度对于代码来说如此重要?
从互联网公司成本来看:
