今天我尝试构建一个神经网络并演示前向传播和反向传播的代码。
首先我们需要创建我们的样本, 由于是监督学习,所以还是需要 label 的。 为了简单起见,我们只创建一个样本进行训练, 可以当做是在模拟随机梯度下降的过程。 代码如下:
x = tf.constant([[0.7,0.9]])
y_ = tf.constant([[1.0]])
我们使用 tf 中的常量来创建样本和 label。 这是一个有两个特征的样本。
w1 = tf.Variable(tf.random_normal([2,3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3,1], stddev=1, seed=1))
b1 = tf.Variable(tf.zeros([3]))
b2 = tf.Variable(tf.zeros([1]))
根据上一节讲的内容,我们使用 tf 的变量来生成权重和偏差。
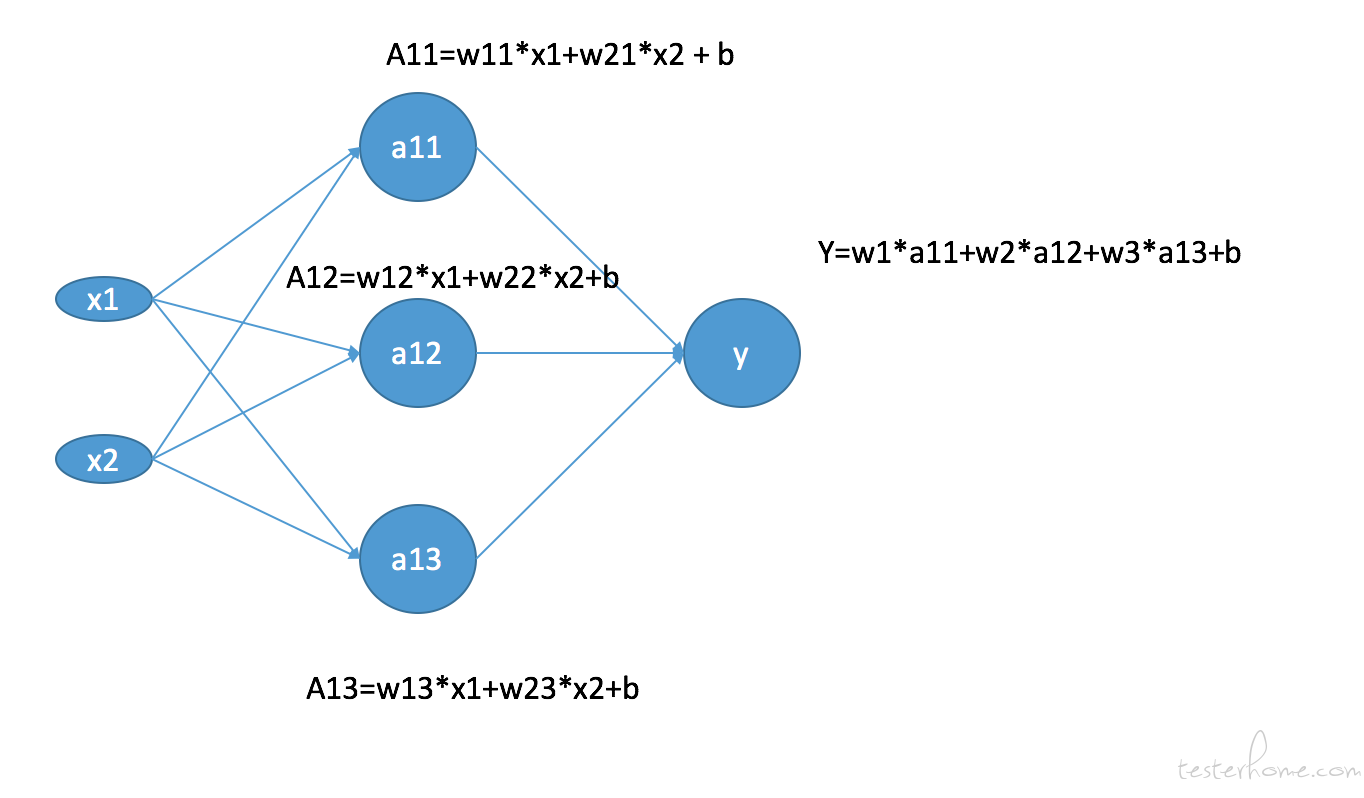
我们的神经网络模型大概如下图:

上面我们尝试创建一个只有两个特征的输入层, 只有一层,3 个神经元的隐藏层,以及最后的输出层。 由于我们要做的是二分类,所以输出层只有一个神经元。
好了现在我们可以来看看前向传播了,如果对前向传播还不太了解的话,请复习一下深度学习的基础概念~ 这里只做简单的介绍。 首先在输入层我们有两个特征输入就是 x1 和 x2,他们都会传递给隐藏层的 3 个神经元中进行训练。每一个神经元都是输入层取值的加权和,就像图出计算的一样,分别计算出 a11,a12 和 a13. 同样的输出层的计算是上一层的每一个神经元的取值的加权和,也正如上图计算的一样。这就是整个的前向传播算法,上一层的计算结果是下一层的输入,以此类推。对数学比较熟悉的同学一定猜到了,权重(w)的计算过程就是一个矩阵乘法。 首先是由 x1 和 x2 组成 1*2 的矩阵, 以及隐藏层的每一个神经元上对应的权重 (w) 组合的 2*3 的矩阵 (2 个输入特征的 w,3 个神经元),他们两个做矩阵乘法就是这一层的前向传播算法,结果是一个 1*3 的矩阵。再接着跟输出层的 3*1 的矩阵 (3 个输入特征的 w 和 1 个神经元) 继续做矩阵乘法。就是最后的结果。 很幸运的是 tf 为我们实现了做矩阵乘法的函数就是 matmul。 那么上面这个前向传播的过程就是如下的代码:
a = tf.nn.relu(tf.matmul(x,w1) + b1)
y = tf.matmul(a, w2) + b2
我们在早期的帖子中说过神经网络的每一层都有一个激活函数,我们分类问题的时候都会加入激活函数来增加非线性效果。那么上面可以看到我们使用 tf.nn.relu 这个 tf 为我们实现好的激活函数来给我们的隐藏层前向传播算法增加非线性。 输出层 y 没有用到激活函数,我们之后会说明。
我们需要一个损失函数来计算我们预测的结果与真实值的差距。 tf 为我们实现了众多的损失函数。由于这我们要做二分类问题,那么我们就需要 sigmoid 作为激活函数,所以我们也要使用 tf 为 sigmoid 实现的损失函数。
cost = tf.nn.sigmoid_cross_entropy_with_logits(logits=y, labels=y_, name=None)
sigmoid_cross_entropy_with_logits 的第一个参数是我们的预测值,第二个参数是真实的值,也就是我们的 labels。 刚才我们计算前向传播的时候再输出层并没有使用任何激活函数,是因为我们 tf 的损失函数中会给输出层加入相应的激活函数。 也就是 sigmoid_cross_entropy_with_logits 已经给输出层加入了 sigmoid 激活函数了。
为了实现梯度下降算法,我们需要进行反向传播计算来求得每一个参数对应损失函数的导数。所幸的是 tf 同样为我们提供了各种优化的反向传播算法。 这里我们使用专门的梯度下降。如下:
train_op = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
GradientDescentOptimizer 是梯度下降的优化算法,参数是学习率,这里我们设置为 0.01。 同时优化目标是最小化损失函数。 所以是 minimize 函数,并且把损失函数作为参数传递过去。
with tf.Session() as sess:
init = tf.initialize_all_variables()
sess.run(init)
for i in range(100):
sess.run(train_op)
print(sess.run(w1))
print(sess.run(w2))
之前的帖子说过 tf 是图计算。 我们之前做的所有的操作都不会产生实际的计算效果。而是在 tf 中维护一个默认的图, 当我们显示的使用 tf 的 session.run 的时候才会去计算整个图中的每一个几点。 上面我们声明一个 Session,并在一开始初始化所有的变量, 循环 100 次代表训练 100 轮迭代。 最后输出训练处的所有的 w。
import tensorflow as tf
import numpy as np
x = np.arange(4, dtype=np.float32).reshape(2,2) # 使用np来创造两个样本
y_ = np.array([0,1], dtype=np.float32).reshape(2,1) # 使用np来创造两个label
w1 = tf.Variable(tf.random_normal([2,3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3,1], stddev=1, seed=1))
b1 = tf.Variable(tf.zeros([3]))
b2 = tf.Variable(tf.zeros([1]))
a = tf.nn.relu(tf.matmul(x,w1) + b1)
y = tf.matmul(a, w2) + b2
cost = tf.nn.sigmoid_cross_entropy_with_logits(logits=y, labels=y_, name=None)
train_op = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
with tf.Session() as sess:
init = tf.initialize_all_variables()
sess.run(init)
for i in range(100):
sess.run(train_op)
print(sess.run(w1))
print(sess.run(w2))
