前几篇一直在讲我们常用的超参数。 使用不同的参数会有不同的训练效果。 但是机器学习圈子里有一句很著名的话大概意思是说再优秀的超参数组合也没有靠谱的特征来的重要。也就是说超参数是锦上添花,特征才是最重要的。 合理的处理和抽取特征比选择超参数甚至是模型算法要重要的多。
我们通常说特征的时候其实是有两种特征,离散化与连续化的特征。什么是离散化特征呢? 就是可枚举的特征。例如性别,要么是男,要么是女,没有别的答案了。 又或者学历:无学历,小学,中学,高中,中专,大专,本科,硕士,博士。 这些都是可枚举的。 而连续化特征就是一些不可枚举的有理数。 例如资产, 从 0 到正无穷你枚举不过来。 我们输入给模型算法的除了目标值 (y 或者说叫 label,也叫标签) 以外就只能是离散的,或者连续的。 那对于机器学习算法来说这两种特征有什么区别么? 答案是没有, 对于机器学习算法,例如 LR(逻辑回归,以下简称 LR), 基本线性回归公式就是:y = w*x +b. 其中 x 就是特征矩阵, LR 并不关心传递进来的特征是连续还是离散。 那为什么我们还要区分连续和离散呢? 答案是这是两种处理原始数据的方式,特征抽取介于数据处理与模型训练中间,是数据通往模型训练算法的最后一道工序,我们需要一些方式来把数据转换成模型训练算法需要的特征。 他们有不同的规则来提取特征,也就是说通过离散化处理原始数据后提取出来的特征跟连续化处理的是不一样的。 举个例子, 假如商品类别这个字段,如果在 100W 行数据中有 0,1,2,3,4,5,6,7,8,9 这 10 钟类型。经过离散化处理这 100W 行数据后,它会变成 10 个特征。换成 LR 的公式就是:y = w1*x1 + w2*x2 +w3*3 ...... w10*x10 +b. 也就是说一旦做离散化处理,他们在 LR 里就是 10 个彼此没什么关系的特征。各自有各自单独的权重。 如果做连续化处理会是什么样子呢? 就是:y = w1*x1 + b。看到了么, 连续化处理后这个商品类型字段只会生成一个特征。它并不会像离散化处理一样对拆出 10 个不同的特征来表示这个字段。 这样不同的处理对于像 LR 这种线性模型来说区别很大。下面我们具体说说。
LR 是一个非常简单的线性模型。 我们再次回顾它的公式:y = w*x + b。 这是一个线性函数。 我们之前说 0 过, 线性函数的表达能力有限, 我们引入激活函数就是为了给 LR 增加非线性关系。能让一条直线变成曲线。这样可以拟合出更好的效果。(也由此才后了后来说的过拟合问题而引入了正则化超参数), 那么离散化和连续化最大的区别是,对一个字段做连续化后的结果就还只是一个特征,而离散化后的这一列有多少个 key(字段可能的值) 就会抽取出多少个特征。 那么第一点就来了, 单变量离散化为 N 个后,每个变量有单独的权重,在激活函数的作用下相当于为模型增加了非线性,能够提升模型表达能力,加大拟合。 第二点,离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30 是 1,否则 0。如果特征没有离散化,一个异常数据 “年龄 300 岁” 会给模型造成很大的干扰, 因为特征值的异常会导致权重也就是 w 的值也会异常。第三,离散特征的增加和减少都很容易,易于模型的快速迭代。 第四, 一定有同学担心特征过多会导致运算缓慢,但是 LR 是线性模型, 我们在内部计算的时候是向量化计算,而不是循环迭代。稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展。 所以不用担心像 GBDT 算法那样,特征多了就跑不动了 (我们都说 GBDT 不能用离散特征不是因为它处理不了离散特征,而是因为离散化特征后会产生特别多的特征,决策树的叶子节点过多,遍历的时候太慢了)。 所以海量离散特征+LR 是业内常见的一个做法。而少量连续特征 + 复杂模型是另外一种做法,例如 GBDT。
这回我们知道了离散和连续的区别,以及他们的应用场景。但数据并不是我们随随便便想离散就离散想连续就连续的。假如你想给资产这个字段做离散化, 每个 key 都是一个特征,那么就会有海量的特征出现,1000 和 1001 以及 999 变成了 3 个不同的特征, 这可不是我们想要的,中间差那么一块钱很重要么? 我们更希望的是在某一个区间内的数字统一映射成一个特征。 例如资产 100w 以下的算穷人特征,100w 到 1000W 算中产特征,1000W 以上的算富人特征。可能这才是我们想要从这个字段中提取出的 3 个特征。所以才有了连续值分桶方法来把连续特征转换成离散特征。把连续特征的区间分成不同的桶进行转化。 同样的离散特征也可以转换成连续特征,可能的做法是把数据按时间字段进行排序,然后根据时间窗口的数据的值把离散的数据转化成一个数字的值。 具体的细节我也不是很清楚。大家可以查查资料。
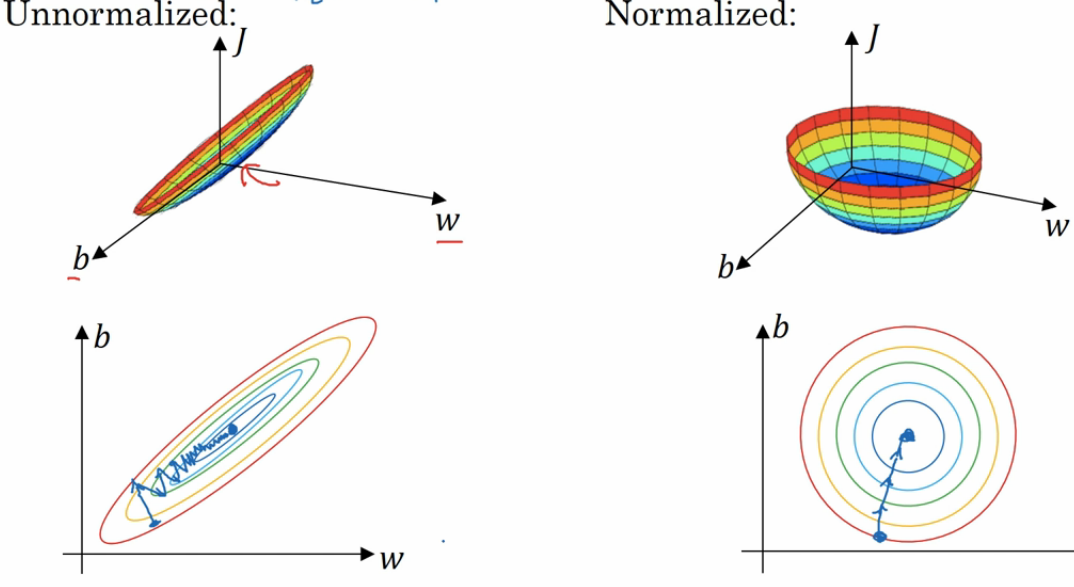
归一化也是一个满重要的步骤。 在我们提取出特征后,我们发现这些特征的值得区间是不一样的。尤其对于连续特征。 特征一的区间是 0~1, 特征二的区间是 0~1000,。那么我们做梯度下降就如下图:

左边是未经过归一化的图,这时候的梯度下降算法有点像一个扁平的碗, 这时候我们需要更多的迭代次数来完成梯度下降。 而右边是经过了归一化的梯度下降,是一个更圆润的碗,我们会更快的进行梯度下降。 那么到底什么是归一化呢, 其实归一化就是把我们的特征值压缩成 0~1 的区间,让所有的特征都处于一个相对平等的状态。如下图:
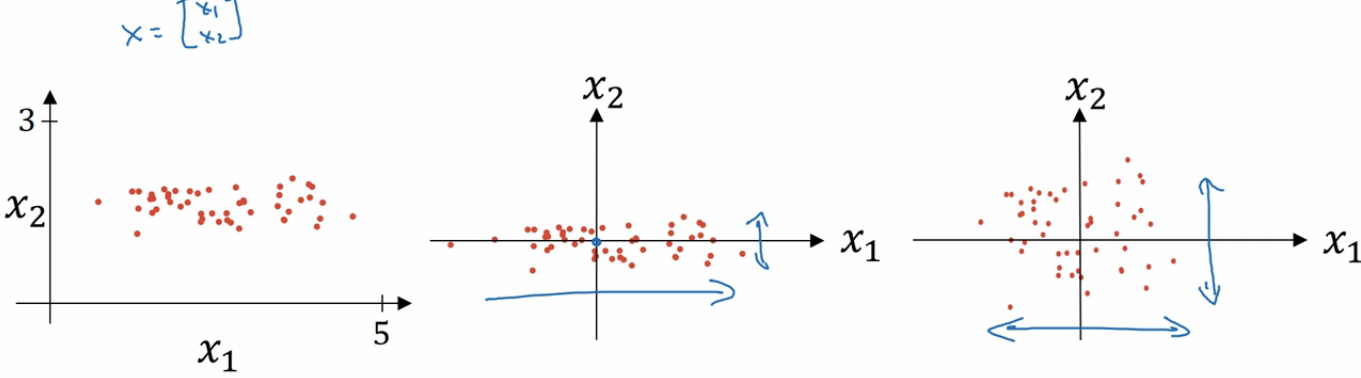
本来特征是在最左边这样分布的,通过归一化,特征的分布慢慢的就变成了最右边的样子。 所以在我们的特征处于不同的分布区间的时候,归一化很有用。 我们在深度学习中,也会有 batch norm 的操作。其实就是把每一层的输出都进行归一化处理后再交给下一层计算。
再处理未经过归一化的连续特征的时候很容易计算溢出,还是例如资产,如果你计算马云的资产的时候,几百个亿的数值运算再经过激活函数的各种方差运算后,很可能超过计算机对 float 的最大区间。 也就造成了计算溢出。假设我们不做归一化处理 (某些情况下,可能不做归一化会更好,目前我还不太清楚),就需要小心的对特征进行抽取,尽量不要引入数值过大的特征。
特征工程是一个非常复杂和讲究的过程。需要对业务十分了解的前提下进行科学的实验。就像开篇说的,好的特征抽取比模型参数要重要的多。
