我们看到我们输入的特征有 size(面积),bedroom(几居室), zip code(邮编),wealth(财富程度)。 然后我们根据面积和几居室可以预测出家庭成员人数。邮编可以预测步行化程度,财富程度可以预测当地学校水平。 图中的每个小圆圈都是一个逻辑回归。 步骤是我们先是用已有的特征通过逻辑回归预测出新的特征。 然后再用新的特征输入给下一个逻辑回归,计算出最后的预测值。 这是一个浅层神经网络的工作流程。当然了这是翻译成人话的,实际上的神经网络其实不是这么人性化的。 看下图:
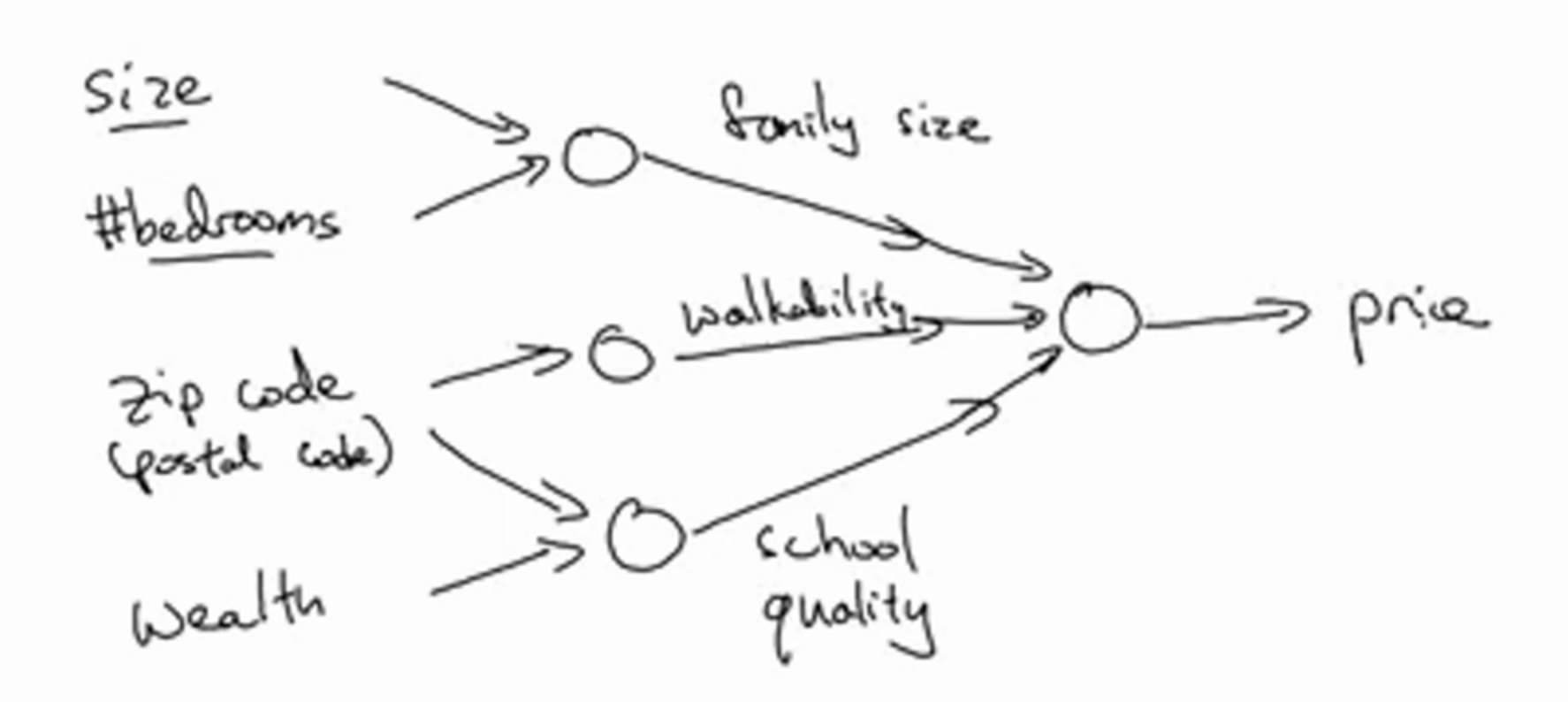
根据上篇帖子,我们知道了逻辑回归这种 2 分类算法。 严谨的说逻辑回归就是只有一个神经单元的神经网络。 而神经网络就是很多个层次的逻辑回归组成的。回顾一下在讲房价预测的例子中我们说求一个函数:y=wx +b,其中 x 是特征向量,y 是预测值。逻辑回归要不停的迭代变换参数 w 和 b 的值以找到最合适的参数来让预测值和实际值相差最小。 在那个例子中我们只有房屋面积这一个特征。 但实际上我们也有其他的特征,例如几居室,当地财富程度,邮编等等。 我们现在用人能理解的大白话模拟一下神经网络是个什么东西。 如下图:

我们看到我们输入的特征有 size(面积),bedroom(几居室), zip code(邮编),wealth(财富程度)。 然后我们根据面积和几居室可以预测出家庭成员人数。邮编可以预测步行化程度,财富程度可以预测当地学校水平。 图中的每个小圆圈都是一个逻辑回归。 步骤是我们先是用已有的特征通过逻辑回归预测出新的特征。 然后再用新的特征输入给下一个逻辑回归,计算出最后的预测值。 这是一个浅层神经网络的工作流程。当然了这是翻译成人话的,实际上的神经网络其实不是这么人性化的。 看下图:
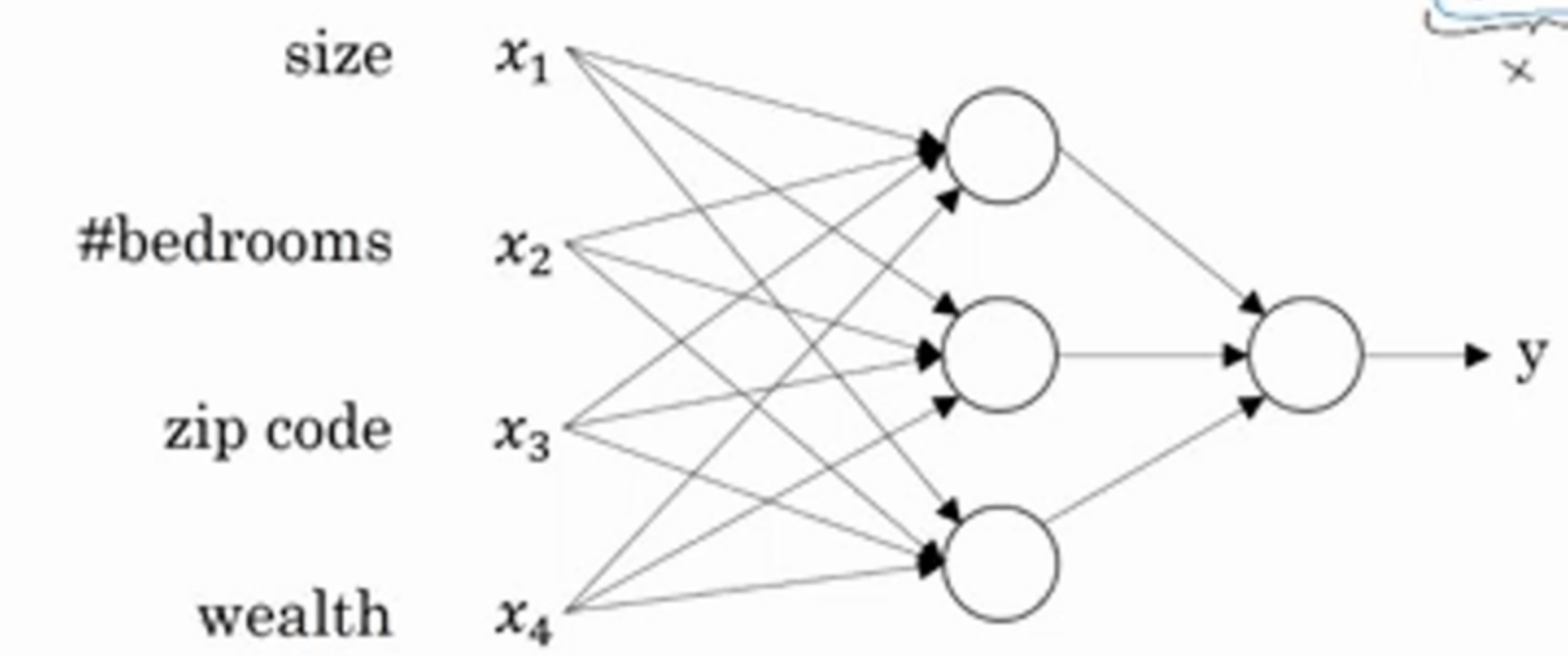
这是刚才的神经网络的结构图。 在最左边是我们输入的特征 (我们称之为输入层),他们都将传递给下一层的每一个节点上,而中间的每一个节点都是逻辑回归。他们会根据上一层的输入特征计算出新的特征 (因为这部分对于我们来说是不可见的,所以称为隐藏层)。 之后我们最终传递给最后一层 (输出层) 计算出预测值。跟刚才的解释不太一样的是,在神经网络中其实我们并不需要指定隐藏层中的哪一个节点计算什么特征。这一部分是自动完成的。计算出的特征也可能是人类无法理解的。
我们在逻辑回归中最后会用一个 sigmod 函数把一个线性转换为一个从 0~1 的非线性关系。 如下图:
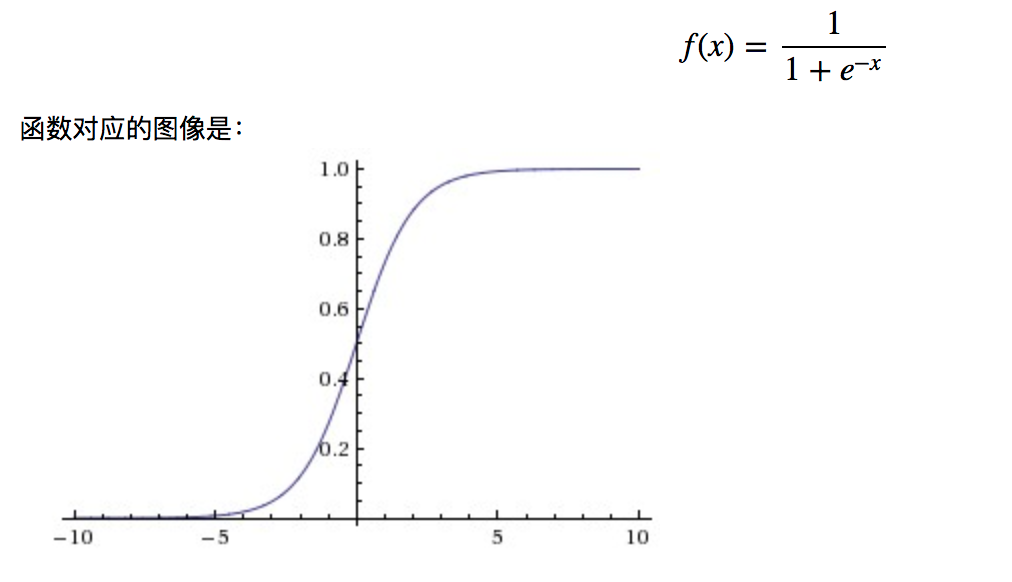
但实际上我们还有另外一个类似的激活函数 tanh
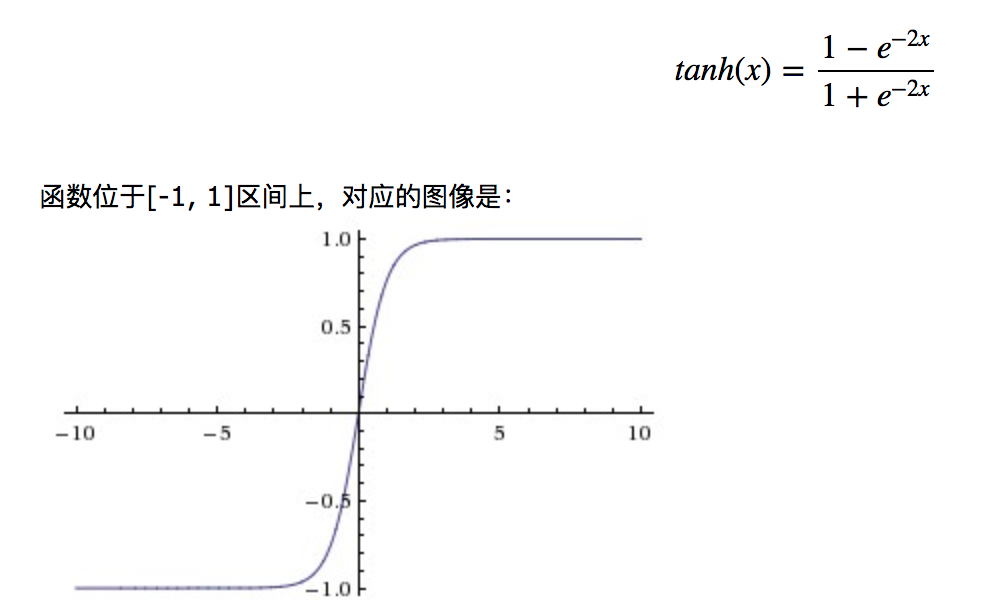
tanh 是一个 sigmod 平移后的函数版本,在隐藏层中我们对每一个节点的激活函数选择往往不会使用 sigmod。而是用 tanh 和 ReLU. 使用 tanh 比 Sigmoid 函数收敛速度更快,相比 Sigmoid 函数,其输出以 0 为中心。这让下一层的计算更容易一些。但他仍然没有解决 sigmod 的一个缺点。 就是在当 z 值 (在逻辑回归中,z = wx + b, y=激活函数 (z)) 很大或者很小的时候,那么对应的导数 (斜率) 会很小 (无限接近于 0)。 上次说逻辑回归的时候我们知道在梯度下降算法中每一次迭代的时候也就是每一次改变 w 参数的值的时候是根据 w = w - 学习率 * 导数。 其中学习率是手动设置的参数,这时候如果导数 (斜率) 过小,会导致梯度下降的的步数也很小。影响效率。 所以我们还有一个激活函数是 ReLU
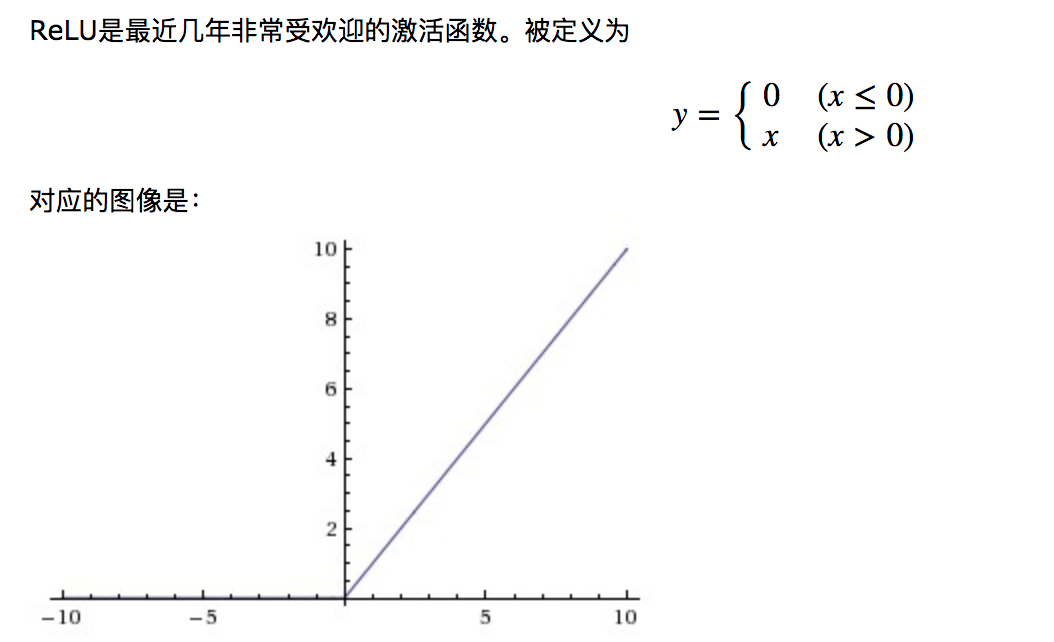
ReLU 最有特点的就是当 z 大于 1 的时候,导数 (斜率) 永远等于 1。而 z 小于 1 的时候无限接近于 0. 这样我们能保证在 z 大于 0 的时候不会出现 sigmod 和 tanh 关于导数过小的问题。但是如果 z 小于 0 的话仍然有这个问题。 所幸如果我们在隐藏层中设置很多个节点的话,就可以有效避免 z<0.
所以总结一下,如果我们做的是 2 分类,那么在输出层中使用 sigmod 是合理的,因为它把函数转换成了 0~1 的数,是适合做 2 分类计算的。而在隐藏层中,我们通常使用 tanh 和 ReLU,一般默认使用 ReLU。
我们在逻辑回归中,一般对于 w 和 b 的值都初始化为 0,但这在神经网络中是不可以的。因为隐藏层中的每一个节点接受到的输入都是一样的,如果 w 和 b 的值都初始化为 0 的话,那么结果将是隐藏层中的所有的节点都是在计算同样的事情。 所以我们要为每一个节点初始化一个随机的 w 和 b
