
人工智能 = 大数据 + 机器学习。
我理解的现阶段的人工智能是使用机器学习算法在大量的历史数据下进行训练,从历史数据中找到一定的规律并对未来做出的预测行为。比如我们曾经给银行做过反欺诈项目。 以前在银行里有一群专家,他们的工作就是根据经验向系统中输入一些规则。例如某一张卡在一个城市有了一笔交易,之后 1 小时内在另一个城市又有了一笔交易。这些专家根据以前的经验判断这种情况是有盗刷的风险的。他们在系统中输入了几千条这样的规则,组成了一个专家系统。 这个专家系统是建立在人类对过往的数据所总结出的经验下建立的。 后来我们引入了机器学习算法,对过往所有的历史数据进行训练,最后在 25 亿个特征中抽取出 8000 万条有效特征,我们可以把这些特征就暂且当成是专家系统中的规则。当时对第一版模型上线后的数据做统计,反欺诈效果提升了 7 倍, 这就是二分类算法典型的业务场景。 为什么叫机器学习呢,因为它给人一种感觉,机器能像人类一样从过去的数据中学习到经验,只不过机器的能力更强。 如果想再稍微深究一下机器学习训练出来的模型到底是什么,我觉得可以暂且理解为一个二分类的模型主要是就是一个 key,value 的数据库。key 就是在数据中抽取出来的特征,value 就是这个特征的权重。 当我们想要预测一个用户的行为的时候,就会从用户的数据中提取特征并在模型中查找对应的权重。 最后根据这些特征的权重算出一个分,也可以说是一个概率。 如果大家看过最强大脑这个节目的话。应该记得第一次人机大战项目是人脸识别,第三回合的时候机器给出了两个答案。因为当时做人脸识别项目的志愿者中有一对双胞胎。所以机器计算出的这两个人的概率只差了 0.1%,最后为了谨慎起见机器输出两个答案出来。以至于吴恩达先生也很纠结到底该选哪一个答案。再之后的人机对战项目里我们也能看到虽然小度一路高歌,毫无败绩。但是其中是有选错过几次的。所以大家可以看到我们得到的答案其实是一个概率,是一个根据以往的数据进行总结并作出预测的一个行为。并不是 100% 准确的。

目前工业界最能产生价值的是机器学习中的监督学习, 场景有推荐系统,反欺系统诈等等。其中二分类算法应用的尤其之多。例如上面的图像识别场景, 我们希望判断图片中是否有猫,于是我们为模型输入一张图片,得出一个预测值 y。 y 的取值为 1 或者 0. 0 代表是,1 代表否。
逻辑回归是二分类算法中最典型的一个。 再说逻辑回归之前我们先说说线性回归。 我们用预测房价这个例子说起。 如下图:
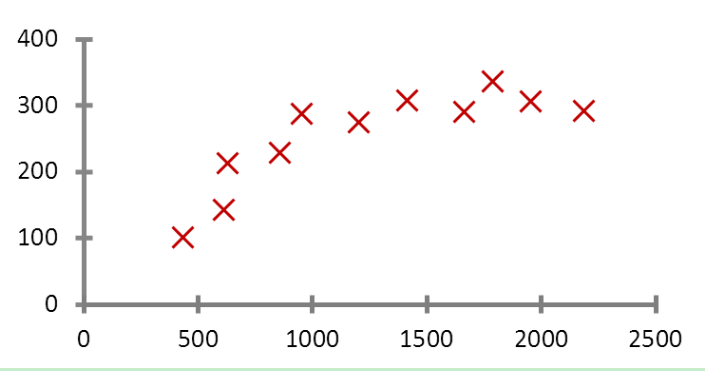
为了方便理解假设影响房价的因素只有面积这一个特征,上面是一个房价随着面积变化的趋势图。我们希望有一个函数, 在输入房价后能得到一个预测的房价数值。也就是 y= wx +b。我们输入 x(也就是面积), 得到 y(也就是预测值)。而机器学习要训练并学习的就是参数 w 和 b。根据梯度下降的原理。 算法在迭代训练中会不停的改变 w 和 b 的指,将得到 y(预测房价) 值于训练数据中实际的值 (实际的房价) 进行对比。 最后找到最优解 (于实际值差距最小的 w 和 b)。所以我们再看 y=wx + b 这个函数,在我们的例子里只有面积这一个特征,所以 x 是一个一维的特征向量 (或者说特征矩阵),在实际中影响房价的可能有多个因素,例如地点,朝向等等。 所以我们的 x 就是多维的特征向量。 我们函数也变成了下面的样子。
假设有 n 个特征,函数就变成了: y = w1*x1 + w2*x2 +w3*x3 ......... wn*xn + b。 之前说暂且将模型理解为是一个是 key,value 的数据库。 key 是特征,value 是权重。 那么这个公式中的 w 和 b 就相当于权重。我们将每个特征和权重进行计算并累加,最后就是我们的预测值。
之所以叫线性回归,因为函数是线性函数。在图中是一条直线。 如下:
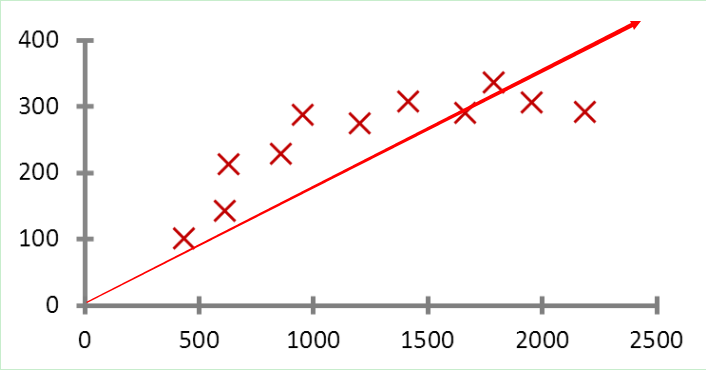
回归算法是用来预测一个具体的值,就像上面我们说的预测房价,也就是 y=wx+b。 而分类算法是在一群实体中将物品进行分类,例如二分类算法中,预测值只有 0 和 1.逻辑回归算法是一个二分类算法,同样用了线性回归公式,也就是 y=wx+b。 但是我们的期望值是 0 或者 1。 所以我们需要一个额外的激活函数来把我们的预测值变换成 0 和 1. 这就是为什么逻辑回归虽然叫回归但却是二分类算法的原因 (它多了一个激活函数把预测值变换成 0 或者 1 的数值)。
激活函数不是真的要去激活什么。在神经网络中,激活函数的作用是能够给神经网络加入一些非线性因素,使得神经网络可以更好地解决较为复杂的问题。例如我们给逻辑回归用的 Sigmoid 函数:
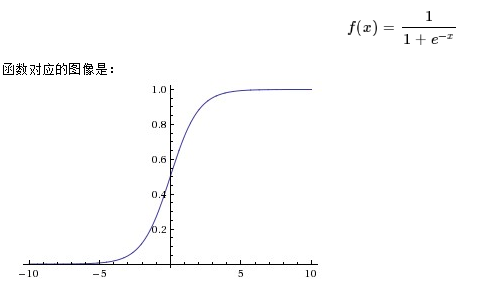
其他激活函数还有 tanh, ReLU 等。
根据刚才学习到的,逻辑回归是一个线性回归加上一个 sigmoid 函数。那么我们的公式就变成了下面的样子:
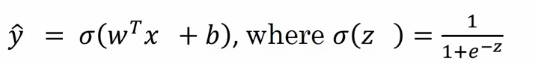
我们之前说的根据梯度下降的原理算法会不停的改变 w 和 b 的值以找到合适的 w 和 b 的值让预测的 y 值跟实际的 y 值差距最小。那么我们就需要一个损失函数来横向我们算法的运行情况。
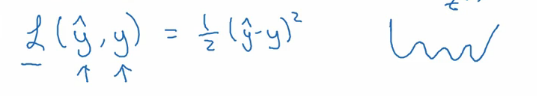
上面是一个可用的损失函数的定义。计算预测值于实际值得方差来量化算法运行质量。 但在逻辑回归中并不会这么做,因为他是一个非凸函数。 就像上图中右边画的一样。 它有多个低谷,也就导致了有多个局部最优解。 我们希望损失函数是凸函数,就像下面的图一样,只有一个最优解

这样我们就有下面的损失函数。
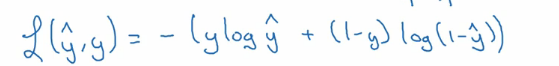
这是计算一个样本的损失函数,但我们的训练数据集是很大的,我们注定了有数百万,数千万甚至数亿的样本。 所以我们需要一个全局的损失函数,也叫作我们的成本函数,如下:
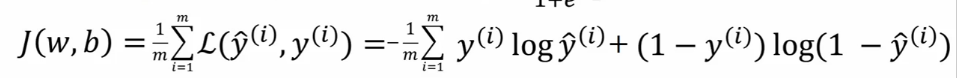
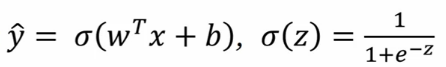
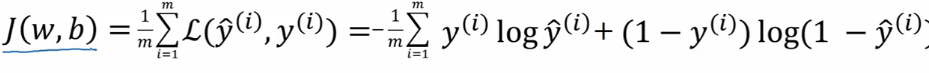
根据上面说的,我们有了逻辑回归算法的公式 (上图 1), 有了全局成本函数来评价算法运行的情况 (上图 2)。 现在我们需要一个方法来迭代式的训练学习到 w 和 b 的值,并用成本函数来判断哪个 w 和 b 是我们的最优解 (可以理解为学习特征权重)。也就是说我们要不停的变换 w 和 b 的值并用成本函数计算预测值和实际值,找到差距最小的,也就是成本函数值最小的那一组 w 和 b。这就是梯度下降算法要做的。
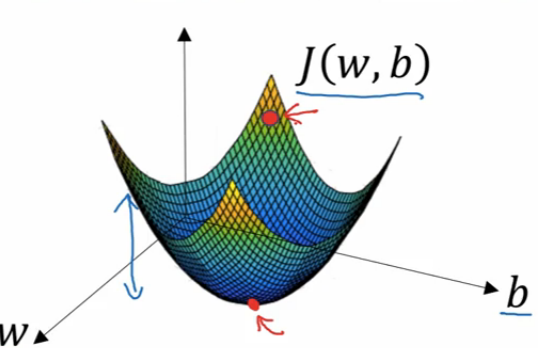
上面是成本函数的图, 可以看到成本函数是一个凸函数,它只有一个最优解。我们要做的就是随便初始化一个 w 和 b 的值 (通常是 0), 也就是图中最上面的那个红点。 然后接下来要做的就是一轮又一轮的迭代,每一次迭代都减少 w 和 b 的值让红点向下走,一直到最下面的那个小红点,或者最接近那个小红点的地方。这也就是我们找到全局最优解的地方。在这里成本函数的值最小。也就是说我们的预测值是最接近实际值的。这样我们的训练过程就结束了,也就是我们学习到了最适合的 w 和 b 的值。
在梯度下降算法中,我们不停的减少 w 和 b 的值来一次次的迭代,那么减少多少是合适的呢? 我们用下面的公式来做。
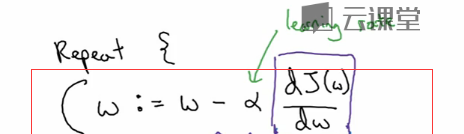
假设我们要算 w 的值,我们每一次都用 w 自身减去α(学习率) 和成本函数 J 对 w 的导数(也就是斜率)。 其中学习率是算法的参数,需要人工设定。
这就是我理解的机器学习中的分类算法中的二分类算法 -- 逻辑回归的原理。这也是构建深度学习中的神经网络的基础算法。
