
本文为「Dev for Dev 专栏」系列内容,作者为声网大后端智能运营算法团队 算法工程师 @ 黄南薰。

本文为「Dev for Dev 专栏」系列内容,作者为声网大后端智能运营算法团队 算法工程师 @ 黄南薰。
随着深度学习技术的发展,编码器的结构在构建神经网络中成为了热门之选,在计算机视觉领域有众多成功案列。声网智能运营算法团队经过调研后发现,经过修改调整后的时序编码器在与时间规律强相关的数据集上展示出很优秀的预测能力。声网的许多业务场景中涉及以运筹算法为核心的资源调度策略,声网深度学习时序编码器模型可以提供高效而准确的预测服务,以支持运筹算法根据未来资源需求进行提前规划。
在声网的众多业务中,许多业务的数据往往伴随着较强的时间规律性,例如泛娱乐场景下一般周末业务会相对较为活跃,教育场景下往往有着相对固定的用量高峰时段。这种跟时间关联在一起的数据一般被称为 “时间序列”。时间序列由于在生活中的广泛应用,关于时间序列的预测一直是经久不衰的话题之一。
声网的业务系统在支持公司业务的同时,也实时记录了这些业务所消耗的各个维度的资源情况。经过探究后发现,只要业务规模达到一定程度,对应的业务的各项资源使用情况就会呈现出或强或弱的规律性特征。声网的通用业务平台提供了超融合基础架构(Hyper Converged Infrastructure),能够从资源池中高效分配、回收资源。对服务未来资源的变更操作,依赖于对该服务未来资源需求情况的精准预测。一旦确定了某个可调度范围内的未来资源需求情况,业务系统可以通过基于运筹算法的调度策略实现资源高效利用,从而降本增效,因此时间序列预测是整个业务资源高效利用的核心,也是保障业务高可用的基石。
在处理时间序列数据时,常见算法是根据数据的时序特征,对数据本身进行分解。进行时间序列分 解时,通常认为时间序列是周期性成分、趋势性成分和残差成分叠加或相乘的产物,即 y(t)=S(t)+T(t)+R(t) 或 y(t)=S(t)×T(t)×R(t),因此,一般会假定时间序列具有较强的周期性,从原数据中将时间序列的周期性和趋势性进行剥离,分别进行预测,最后根据残差来得到一个预测的时间序列未来的可能值范围。声网智能运营算法团队在进行时间序列的分解时经常发现,常见的按周期和趋势分解时间序列进行预测的方法会遇到周期固化,异常波动难以处理,不确定性预测难以实现等各种问题。
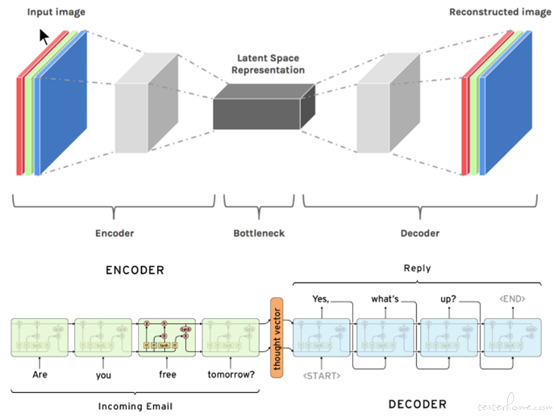
■计算机视觉和自然语言处理中常见的自编码结构
在特定的场景下,传统的机器学习算法无法到达较好的预测效果,这时候深度学习便成为了最优之选。深度学习的许多经典场景集中在计算机视觉和自然语言处理上,核心目标是提取出输入部分的关键信息,制定合适的优化目标,得到期望的目标结果。既然图像与文字均能够通过合适的变换,提取出特征信息,带有时间标签的数据也不应当例外。声网智能运营算法团队经过探索后发现,时间序列数据经过合适的预处理方案,通过特定的模型结构与特殊的预测方式,可以在各种业务的各个资源维度上均取得较好的预测结果,继而提出了两个通用解决方案:通用资源时序自编码器 GRTAE(General Resource Timeseries Auto-Encoder) 和通用资源时序变分自编码器 GRTVAE(General Resource Timeseries Variational Auto-Encoder)。
算法详解
常见的时间序列分解方法一般会采用类似 STL(Seasonal and Trend decomposition using Loess)² 的思想,通过回归、平滑、过滤等方式挖掘出时间序列的周期性,在处理周期、趋势较为明显的时间序列数据的时候,通过分解、分别预测、重组的方式来得到一个时间序列的预测结果相比 ARIMA(Autoregressive Integrated Moving Average)等单纯通过回归的方式来进行预测,往往要来的更准确一点,同时也能够通过分 解后的残差得到一个较为合理的置信区间。
算法潜在问题
时间序列的规律并非一成不变的,截止到哪部分的数据适合用来当作预测数据往往会成为一个较大的难点。由于趋势性的部分往往是通过分段并采取线性的方式进行预测的,当遇到趋势性非线性的时候往往会和周期性难以区分,导致训练过拟合。而进行相对较长的未来预测的时候由于模型鲁棒性较差,一旦出现规律发生微小变化,就会产生一定误差,而这部分误差作为历史数据进行滚动预测的时候便会导致误差被放大,最后整个预测趋势会变得难以挽回。如下图中使用 Prophet³ 进行预测遇到的误差放大就是常见的情况。
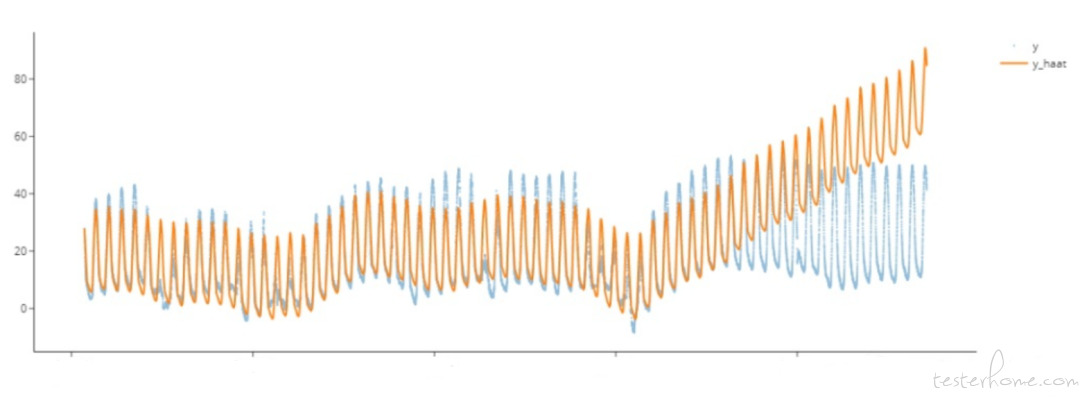
■时序分解中误差放大的情况
03 通用资源时序自编码
模型介绍
自编码这一概念最早诞生于 1986 年¹,随着神经网络技术的发展,在计算机视觉与自然语言处理中都发挥着重要的作用。自编码器的核心在于通过编码层将输入数据的高维特征进行抽象化的提取,再通过解码层将这些特征进行表达。为了尽可能保证信息的还原,编码器和解码器的结构往往是对称或近似对称的。
通用资源时序自编码器 GRTAE 跟常规的自编码器一样,分为编码器和解码器两个部分。模型会要求定义好输入和输出窗口大小,对时间序列数值及时间进行窗口化的划分,并在窗口中进行预处理,作为训练时的特征和预测时的输入值。异常值的过滤也会在预处理的过程中同步完成。
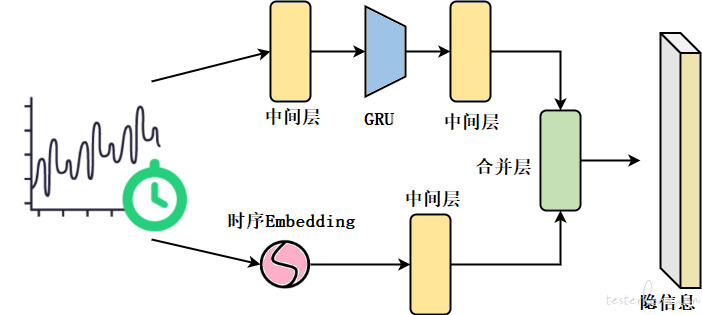
■GRTAE 编码器部分结构
模型的编码器部分会同时接收时间序列的时间值及数据值,分别进行特征的抽象化。模型中的中间层部分并不相同,但结构相似,通常为由数个全连接层、激活函数层、池化层和随机丢失层组合而成。数据值部分会先经过中间层,再经过一层循环神经网络 GRU(gated recurrent unit),再经过一次中间层;同时时间部分会经过一次特征嵌入 Embedding,再经过一层中间层。两部分分别处理过以后会分别得到形状相同的两部分张量,合并层会将两部分张量连接,并再经过一层全连接进行变换,得到训练完成的隐信息部分。

■GRTAE 解码器部分结构
模型的解码器部分和编码器部分采取的各个子模块都是相似的。首先将隐信息输入到中间层,经过 GRU 层备用,同时将要预测的部分的时间提取出来,经过一次特征嵌入后输入至中间层。再将这两部分合并,最后输出一次中间层得到预测窗口中的数值信息。
模型局部细节详解
模型的中间层中会选择性地加入一个或多个激活函数层、池化层和随机丢失层。通常中间层都是以全连接层作为起始层和终止层,但在经过循环神经网络后一般会直接使用激活函数层作为起始层。中间层一般起到增加模型表达力和鲁棒性的作用,实践表明,该网络架构具备较强的鲁棒性和通用性,适用于多个业务场景,预测效果得到保证。
时序嵌入 (Embedding) 有多种方式,我们一开始参考了 Transformer⁴ 中的 positional encoding 的思想,用正弦和余弦的三角函数变换后进行交替编码,并在原方法上做了简化处理,得到了通用便捷的时间序列嵌入方案。同时经过研究我们也发现,如果采用适当的结构直接引入位置信息,也可以达到和三角函数相仿的效果,这也同时证明了时序部分的合理嵌入方式可以是多样的。
模型优势
通用资源时序自编码器 GRTAE 相比于其他编码器模型较为轻量。在实践中,如果需要预测未来十五分钟的数据,只需要两周的历史数据作为训练集,预测时使用四小时的历史数据,在模型前端增加合适的预处理方式,后端增加合适的平滑方式,就能够将预测窗口内的误差控制在 5% 以内。
由于整个窗口都是由单次预测直接完成,待预测位置上的点除了位置信息外,本身的预测结果没有被作为中间值引入下一次预测。这种非自回归式的预测方式能够有效避免发生传统时间预测算法的误差放大现象。
模型效果展示
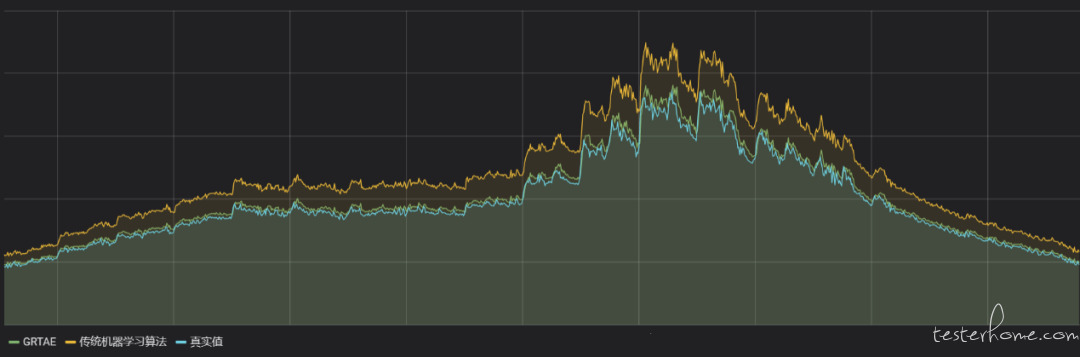
■GRTAE 在资源预测领域的效果展示
图中展示的是 GRTAE 算法在资源预测领域的效果。黄色曲线是传统机器学习算法的预测结果,绿色部分是 GRTAE 的预测结果,蓝色部分是真实值。不难发现,传统机器学习方法在整体趋势上基本能够贴合真实数据,然而一旦局部发生波动或者骤升骤降,算法就会产生较大的误差。然而 GRTAE 则能在一定程度上提前感知到这种变化,及时修正预测结果,和真实值曲线贴合紧密。
模型介绍
通用资源时序变分自编码器 GRTVAE 则是在结构上参考了变分自编码器的结构⁵。由于变分自编码器的结构是在自编码器的结构上修改而得到的,而自编码器在上文已经做过介绍,此处就不再赘述,将编码器部分和解码器部分作为整个整体直接说明,并着重介绍 GRTVAE 与 GRTAE 之间的不同点。首先,在 GRTVAE 中,时序数据不再通过位置嵌入的方式传递,而是通过固定的方式转换成矩阵,和数值数据一起进入编码器。由于将时间特征直接引入,编码器中采用了 Transformer 里经典的自注意力机制 (Self-Attention),用以建立关键特征之间的联系。训练和预测过程采用重参数化技巧(reparameterization trick),对标准正态分布进行采样,将预测问题转化为生成问题,得到数据分布,从而较为容易地计算预测结果置信区间,缓解异常波动带来的预测误差较大的问题。
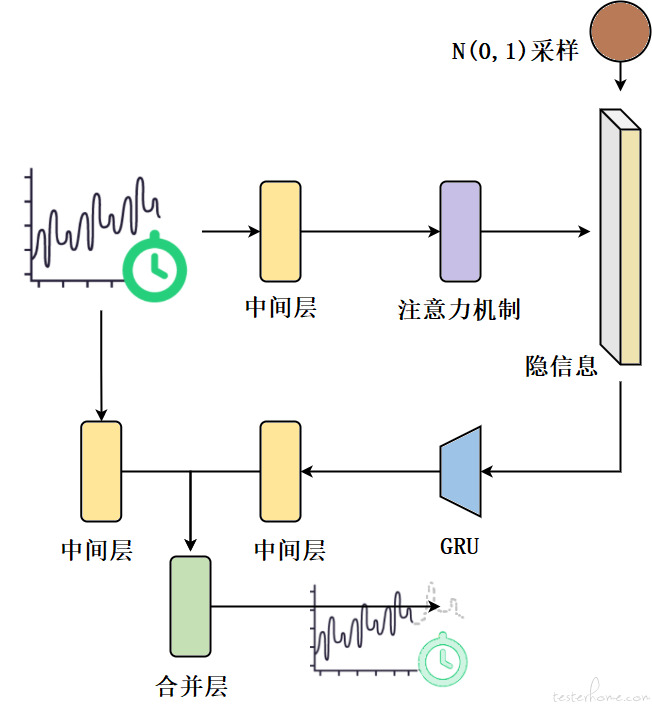
■GRTVAE 整体结构概括
模型局部细节详解
通用资源时序变分自编码器 GRTVAE 的编码器部分引入了自注意力机制。自注意力机制在自然语言处理及计算机视觉中都有广泛的使用,主要通过改变权重的方式让模型自行学习输入中比较重要的部分,比如句子中的关键词或图片中的关键部分,在时序相关数据中则是学习能够决定未来走向的时间和对应的数据。
解码层除了使用长期信息以外,还会从原始数据中拉取一份短期数据,并训练成为包含短期信息的张量,将长短期信息做融合后协同预测。充足的长期数据有助于发现时间序列中的规律,但在规律性上的过渡聚焦会导致算法在预测时只会机械化的参考最类似的场景,而现实生活中的时序数据除了和历史的规律有关外,往往也和最新时刻的状态有紧密关系。短期信息的重复引入有助于这种关系在模型中得到恰当的发挥。
GRTVAE 的解码器部分在预测时获取的短期数据与使用的长期数据均为历史已知数据,同样不采用自回归的方式以规避误差放大的风险。
数据的预处理阶段,进入解码器前的数据还经过了数据滤波平滑和一阶差分预测的处理,这两类处理方式也是时序预测中的常用技巧,和自注意力机制一样,在帮助模型集中学习数据规律性部分上起到了较大的作用。数据滤波平滑可以帮助消除曲线中的随机残差成分,同时会保留数据中的高频信号部分,即时间序列中的骤升骤降的成分,削弱了随机误差对模型训练及预测的干扰。另外,经过测试发现,在使用 GRTVAE 的过程中,比起训练数据本身,将滤波的数据经过一阶差分处理来训练数据的增量部分能够得到更准确的结果。
模型优势
通用资源时序变分自编码器 GRTVAE 由于引入了概率模型,能够直接通过统计学方式生成业务需要的置信区间,这在通用资源平台中资源容量分配及其他很多需要用到预测算法的业务场景中都有广泛的应用场景。
通过注意力机制获得隐向量的方法具有很高的鲁棒性,也就意味着在相似业务上能够进行快速地迁移。模型可以通过迁移学习等方法在相似场景小以极小的训练代价进行快速地复用。
模型效果展示
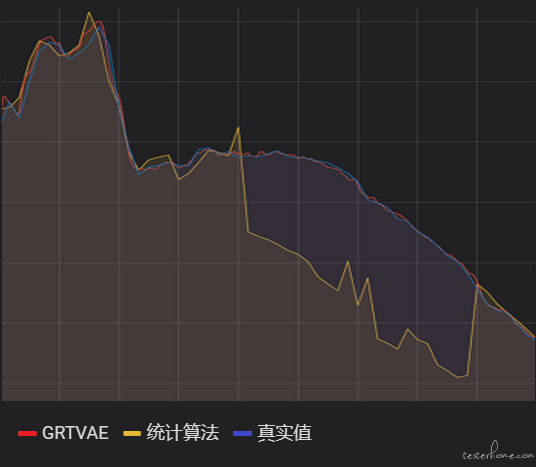
■GRTVAE 在资源预测领域的效果展示
图中展示的是 GRTVAE 算法在资源预测领域的效果。黄色曲线是统计学算法的预测结果,红色部分是 GRTVAE 的预测结果,蓝色部分是真实值。图中选取的时刻是曲线的规律性发生变化的时刻,平时原本会以凹陷形式下降的数值呈现了凸形的下降方式。统计学算法参考了过往同一时刻的值,采用了加权平均,局部回归等思想,但这些方法无法对新的规律变化产生感知。而 GRTVAE 则敏锐地发现了曲线短期信息中包含的差异性,给出了合理的预测结果。同时统计学方法受历史极端值影响较强,故经常呈现出数值的突升突降,而 GRTVAE 由于其依靠分布而生成的原理,得到的是平滑且稳定的预测结果。
声网智能运营算法团队在时间序列数据预测任务的实践过程中,尝试了业界比较优秀的算法,如 DeepAR、Uber 的基于 Dropout 的 Uncertain 和 confident 预测、NBeats、Transformer 系列如 autoformer 等,总体上这些算法在我们的场景里精度和复杂度都难以满足需求,因此我们在借鉴业界优秀成果的基础上研发了适应声网场景的通用资源时序自编码器 GRTAE 和通用资源时序变分自编码器 GRTVAE 两种时间序列预测通用解决方案。单维度的时间序列预测问题在业界一直是一个难以攻克的难关,常见的时间序列预测模型往往在长期周期性与短期趋势性之间难以找到平衡点,同时又会受到滚动预测的思想的影响难以产生稳定的预测结果。经过算法团队的测试,只需要采取合适的预处理方式和输出优化方案,这两套解决方案可以应对各种规模、各种类型的单维度时间序列,也支持拓展到多维时间序列预测上,与一些其他深度学习解决方案相比,又有着鲁棒性强、轻量化、需求样本少等各种优势,能快速满足大部分业务场景的需求。
声网的资源预测场景采用了两种新的编码器方案作为预测模块以后,真正做到了在各个服务各个粒度上,对未来短时间内的资源使用情况有一个较为精准的预测范围,不管是强周期性的时间序列还是骤升骤降的时间序列,都能够参考历史场景及实时趋势,给出合理的预测值。通过将预测算法与以运筹算法为核心的资源调度策略相结合,声网真正意义上实现了随用随取的 “资源自由”。
