继续 parser.

预测 parser

LL(1) 文法
第一个 L left-to-right,第二个 L left-most derivation，目前的 k 都为 1，因为=2 的时候效率满足不了，也可以通过设计关键字来规避。

和回归下降的对比

并不是所有的文法都可以预测，如下图的文法就难以预测

因此引入 left-factor

left-factor(左共因子提取)

左共因子提取的思路是将后续有分支的处理延后，增加非终结符（如上图的 X/Y）。

LL(1) 的执行

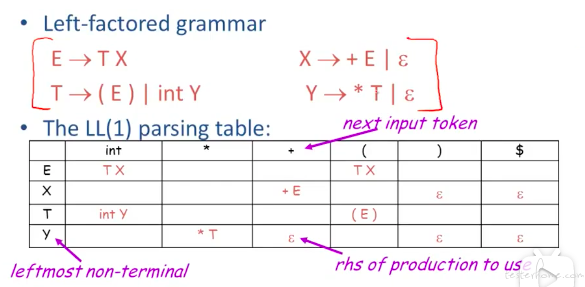
伪代码：

这里分为终结符和非终结符两种情况进行分析。
举例：

单步分析，匹配加弹出。

First Set

First 和 Follow 的定义和解释：

First Set 的定义以及存在的三种情况：

示例：

终结符就是其本身。非终结符按照前面说的算法进行计算。

Follow Set

Follow set 的定义和引理：

这里还有 3 个扩展需要注意：

范例：

LL(1)

parsing table 生成：

举例说明：

非 LL(1) 语法举例：

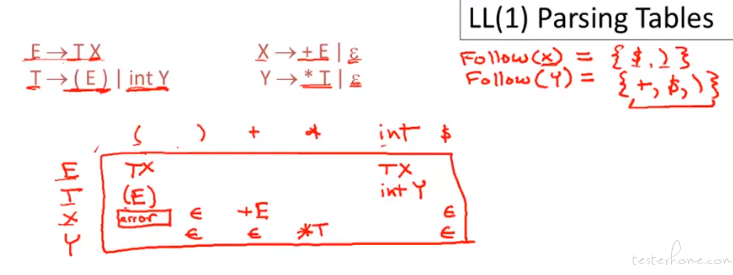
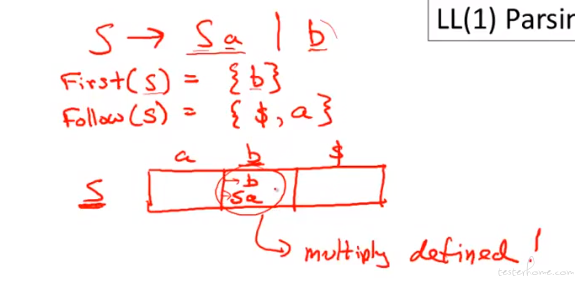
LL(1) 的限制很多，大部分语言都不是 LL(1)

Buttom-up parsing

真正实用的解析器中大部分都是 Buttom-up。

Buttom-up 也不需要提取左公因子

举例：

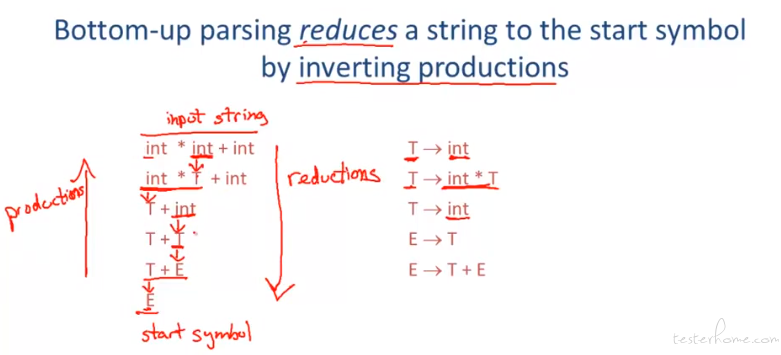
一个原则，自底向上的方法都是替换最右侧的叶节点。

Shift-reduce parsing

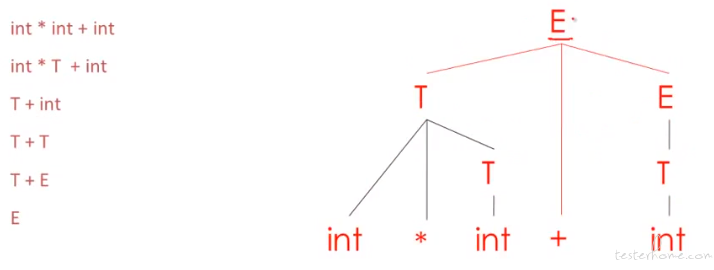
理念：

移动动作：

Reduce 动作：

举例说明：


可能存在的问题：

shift-reduce 冲突可以通过优先级解决。

handles

接着上面讲 shift-reduce 的方法。

核心问题就是什么时候做 shift，什么时候做 reduce。

handle 的定义：

只在 handle 的点做规约：

后续将介绍怎么找到 handle.
handle 在自底向上的解析中，只有存在于栈顶。
关于为什么 handles 只存在于栈顶的简单说明：

识别 handles

CFGS（上下文无关文法）的相互关系：

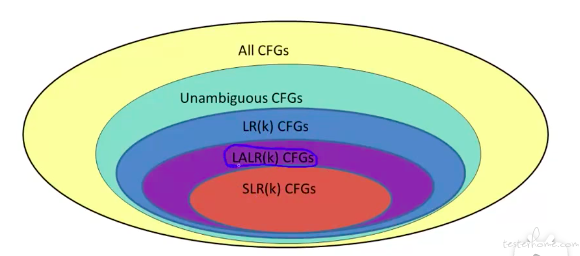
一个定理：

shift 操作后的前缀都是正则语言。

举例说明：


换个例子（int*int）：

识别 valid prefix

继续将识别 handles 的问题转化为识别有效前缀的问题：

这里是真的绕。我是这么理解的：
检测 valid prefix 在于，如果 valid prefix 成立，那么就意味着表达式可以继续往下递归，那就继续压栈继续堆。。。

例子：

对应的 NFA 转化图：

valid item

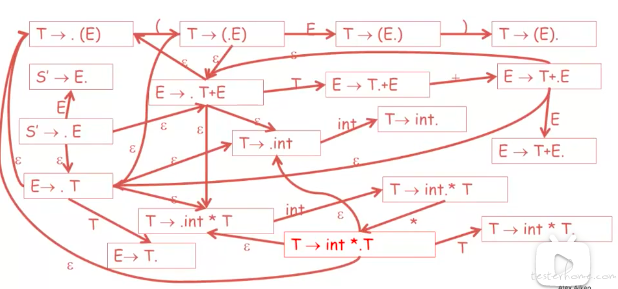
定义：

对于连续的（前缀：

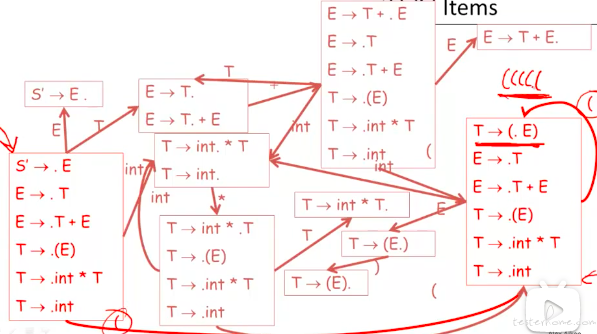
在 DFA 中除了初始态跳转外，其他的的时候自己闭环。

SLR

SLR 是建立在 valid items 和 valid prefixs 基础之上的。

LR(0)

存在的问题：

SLR 定义

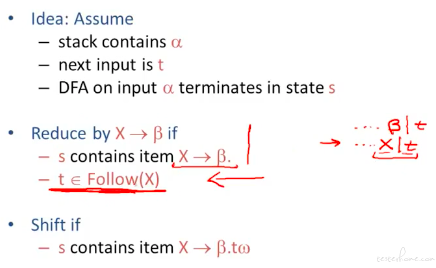
相比于 LR（0），只增加了一条约束条件。
通过优先级可以解决部分 shift/reduce conflict。

优先级并不能解决所有问题。

SLR 实现思路：

SLR 例子：

DFA 示例，相比于前面的图，加了定义的状态编号。

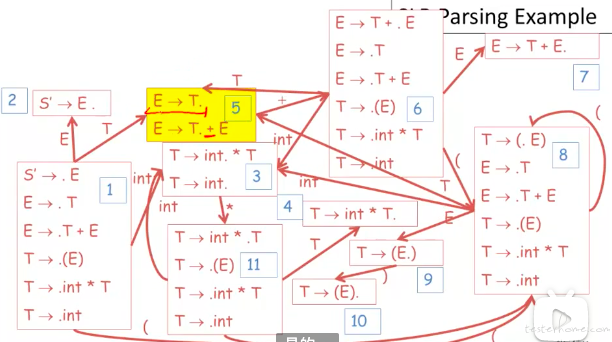
对应的步骤：

SLR 伪代码：

SLR(1) 过于简单，通常还是会使用 LR(1)。
简要介绍：

这里从 LL(1) 的文法讲到了 reduce-shift 方法，讲到了 handle，讲到如何识别 valid prefix 和 valid item，最后再介绍 SLR。
语法分析的主要内容结束，看视频和看龙书都很抽象，我因为时间和能力问题，这一遍也只能简单扫扫。
PS：现在的重点好像都不在词法和语法上，这就是基础。