L5 Tree Computations
Wyllie’s algo
为了实现:
Given a link list, compute its rank.
Do this with using scan or prefixsum n parallel using pointerjumping,known as Wyllie’s algo.
There is at least one trick to make Wyllie’s more work optimal.
- Shrink the list to size m < n.
- Run Wyllie on the smaller list. O(m log(m))
- Restore full list and ranks
The question now is …. how should m be chosen to lead to workoptimality? n/log(n)
个人理解为了实现 Wyllie’s algo,这里主要是针对第一步进行说明,如何将 list shrink 到 m 长度。
Parallel Independent Sets, Part 1: A Randomized Algorithm
首先需要生成一个 Independent Sets。
因为都是并行计算,所有的操作也需要并行。
具体算法实现:
A scheme is needed to break the symmetry.
For each node flip a coin. Heads Pr[heads] = Pr[tails] = ½
Heads will be included in the independent set and tails will be left out.
There is a possibility that a node and its neighbor are both heads.
In this case change the head into a tail, so any head is adjacent to a tail

shrink
初始值:
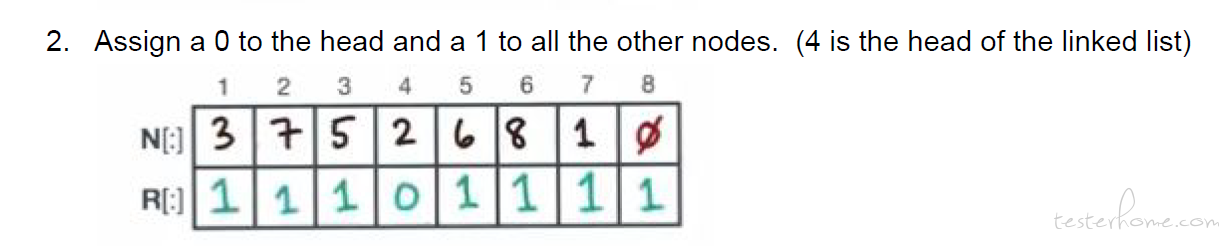
第一步获取 Independent Sets 为 [1,4,8]
去除 1,4,8 节点
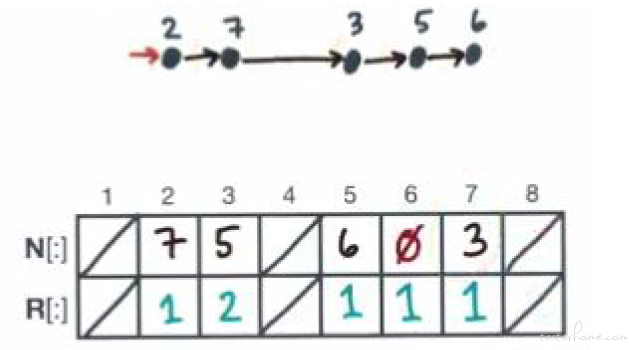
为什么 3 对应的 R 变成了 2?因为 1 在 3 之前,去掉 1 的时候 R 需要 +1
第二步去掉 [7,5]
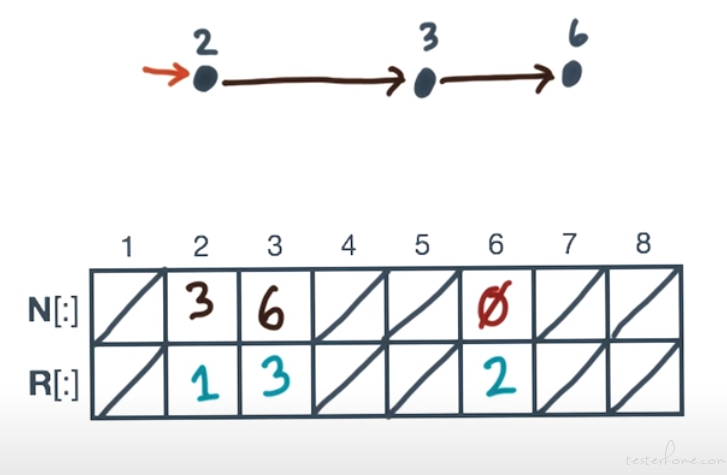
RUN LIST SCAN:
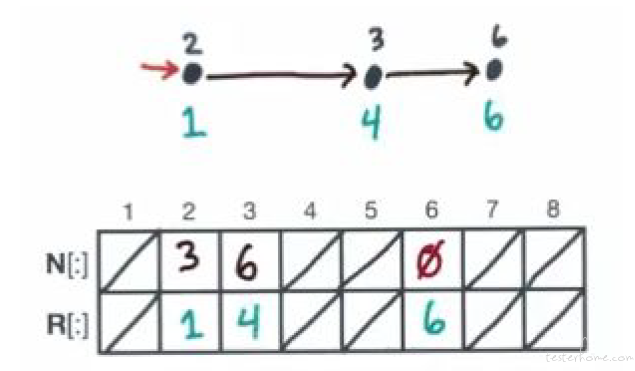
和实际操作一致。
W 1 = O(n log log (n))
D 1 = O(log(n)
A Seemingly Sequential Tree Algorithm
为什么要把图变成 LIST?因为 LIST 可以并行~
Euler Tour Technique
后续遍历通过欧拉图计算:
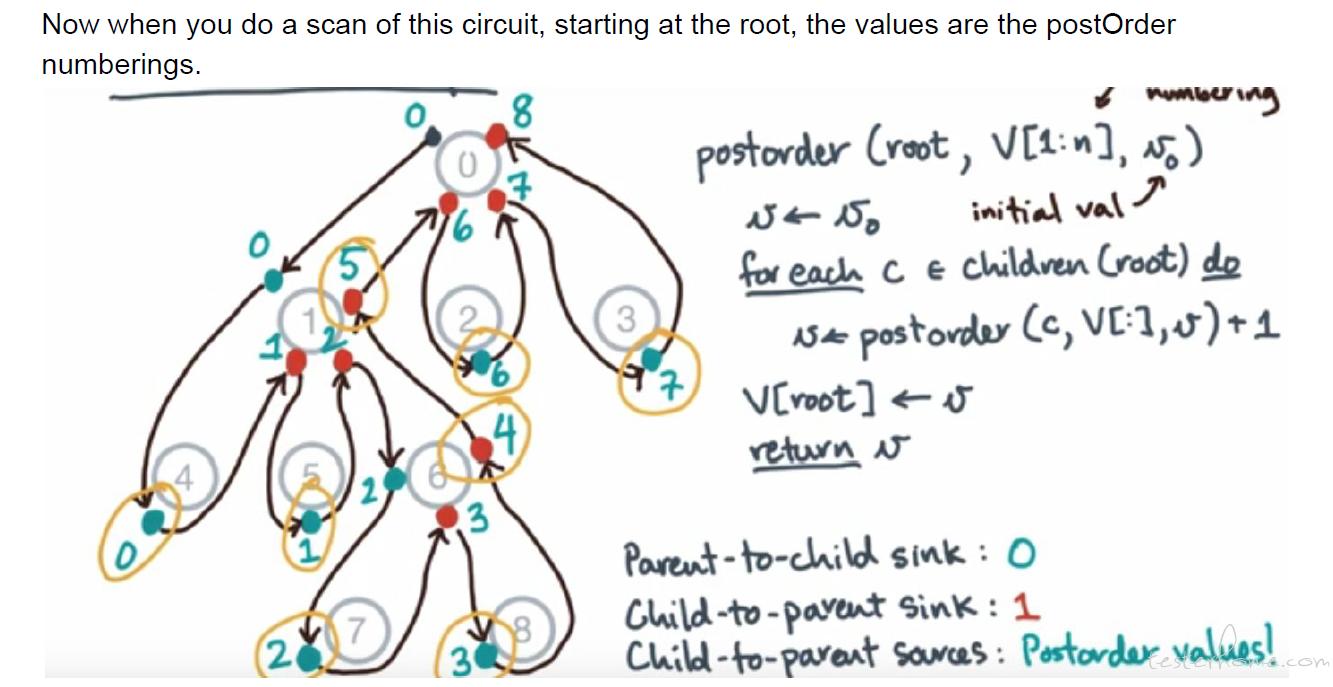
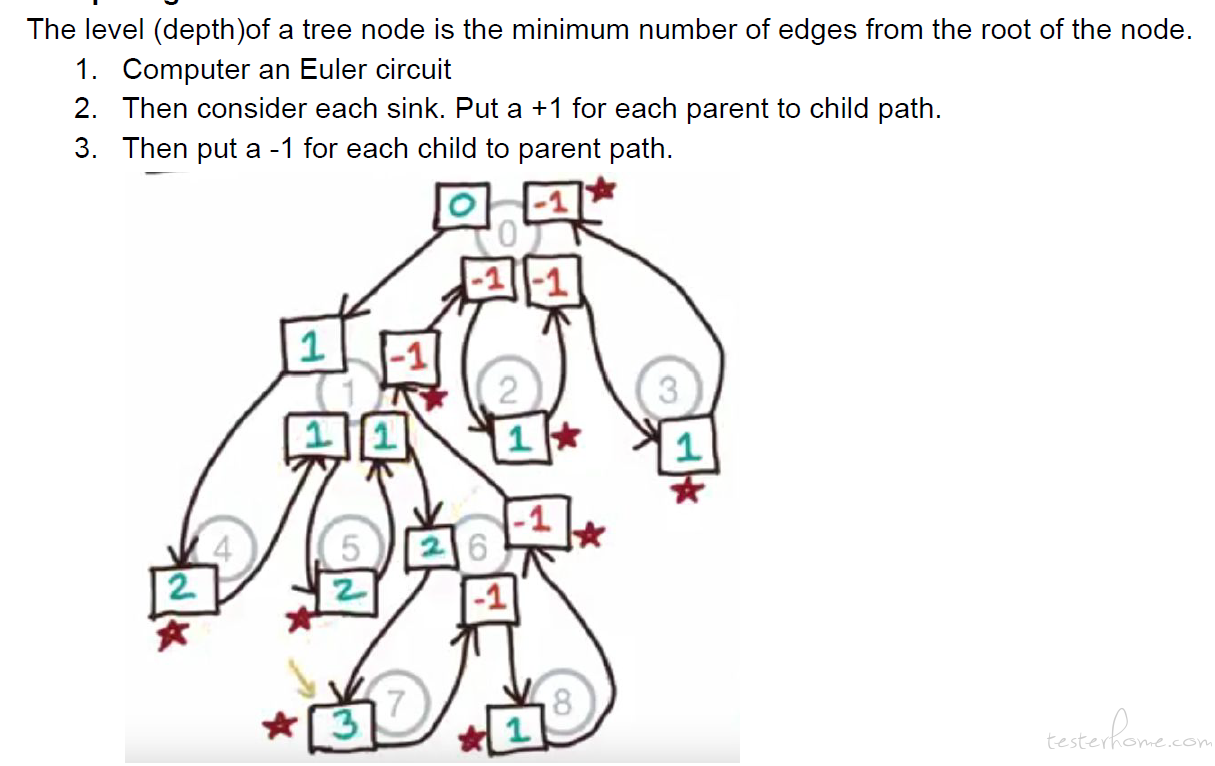
图深度计算:
https://s3.amazonaws.com/content.udacity-data.com/courses/gt-cse6220/Course+Notes/Lesson1-5TreeComputations.pdf
L6 Parallel BFS
BFS 算法:

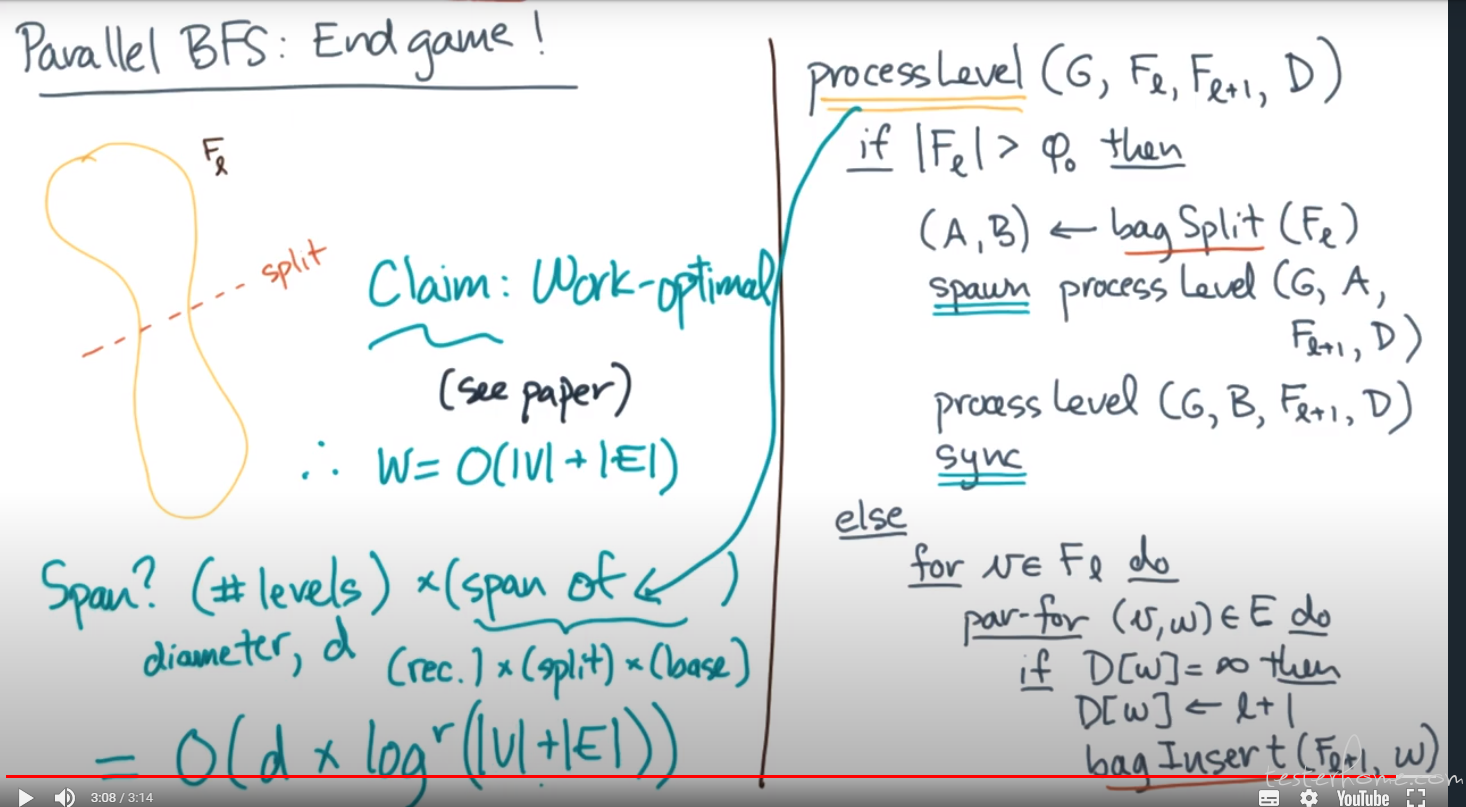
High Level Approach to Parallel BFS
- Carry out the BFS level by level (not vertex by vertex)
- Process the entire level in parallel we can do this because the order in which the
vertices are visited should not matter.

Pennant 概念:

Bags:
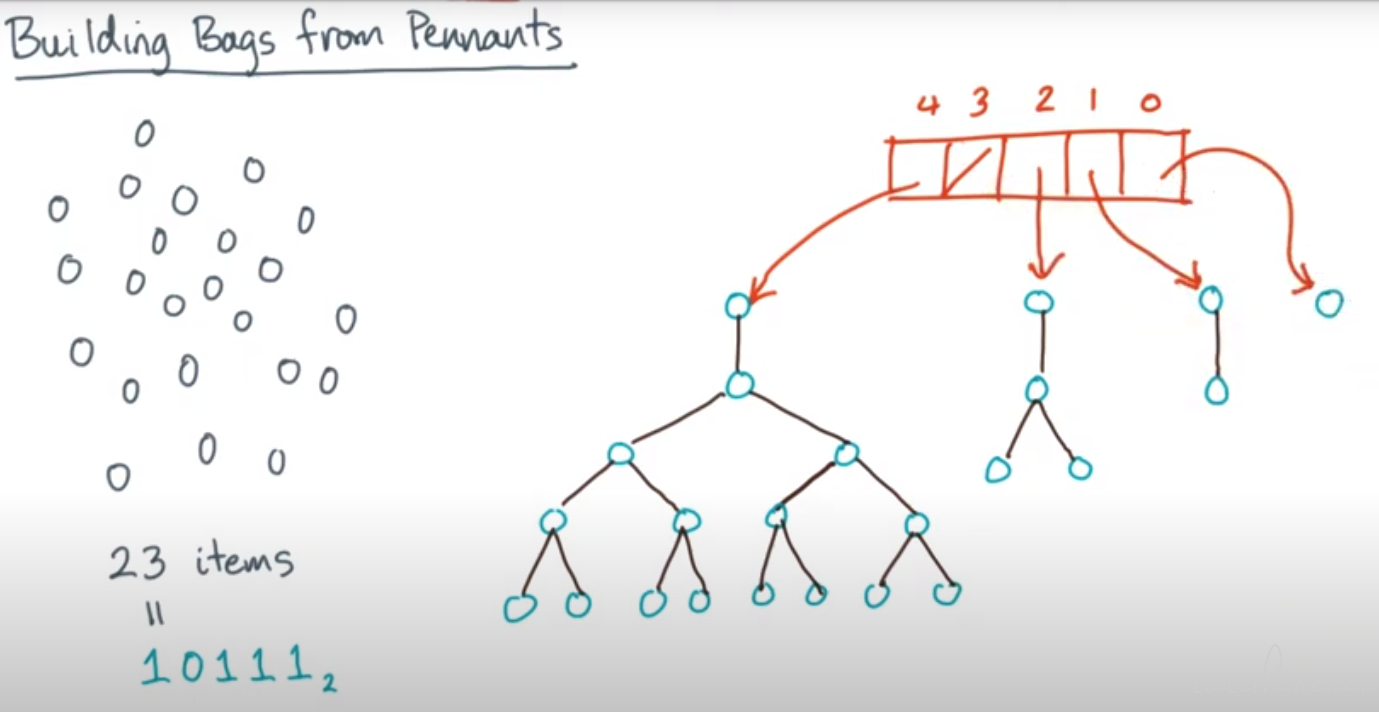
bag 只能对 size 一样的 Pennant 进行合并。
这是基于 2 进制的处理。
Parallel BFS with Bags:
文档:
https://s3.amazonaws.com/content.udacity-data.com/courses/gt-cse6220/Course+Notes/Lesson1-7+Parallel+Pointers+Graphs.pdf

↙↙↙阅读原文可查看相关链接,并与作者交流












