DAG = Directed Acyclic Graph
https://baike.baidu.com/item/%E6%9C%89%E5%90%91%E6%97%A0%E7%8E%AF%E5%9B%BE/10972513?fr=aladdin
Work = number of vertices in the DAG = W(n)
Span = longest path through the DAG = D(n) = number of vertices on the longest span
Span is also known as the critical path.
T1(n) = W(n)
Tinfinity(n) = D(n)
Span Law → Tp(n) >= D(n)
Work Law → Tp(n) >= ceiling of W(n)/P
Tp(n) >= maximum of {Span Law, Work Law} = {D(n), ceiling of W(n)/P}
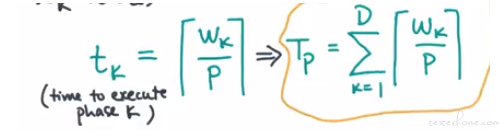
How long will it take to execute phase k?

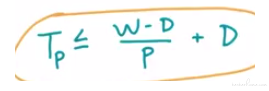
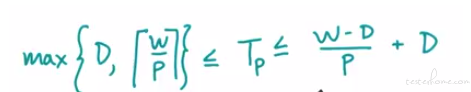
How can we tell is a DAG is good or bad.
Speedup = best sequential time/ parallel time = Sp(n) = T*(n) / Tp(n)
T*(n) → depends on the work done by the best sequential algorithm
Tp(n) → depends on the work, the span, n, and p
Sp(n) = Theta(p) = Best Sequential Work/ Parallel Time = W*(n)/Tp(n)
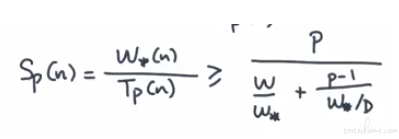
To get a constant in the denominator:
W = W* → Work Optimality
Weak Scalability
P = O(W*/ D) → W*/P = Omega(D) → work per processor has to grow proportional to the
span. Span depends on problem size n.
https://computing.llnl.gov/tutorials/openMP/#Introduction
OPENMP 比 MPI 简单一些。理解一下共享内存和独立内存设置。
